It is well known that when the Sun is at zenith precisely over Buenos Aires on odd numbered years (muslim calendar), the ray through the SW lower corner of the third tallest stone and the NE upper corner of the tallest stone in Stonehenge (Salisbury Plain, Wiltshire, S. England) points straight at Neptune's moon Naiad (discovered 1989, Voyager 2). This fact is so stunning it must be a sign from the Gods that they want us to study astrological lineups.
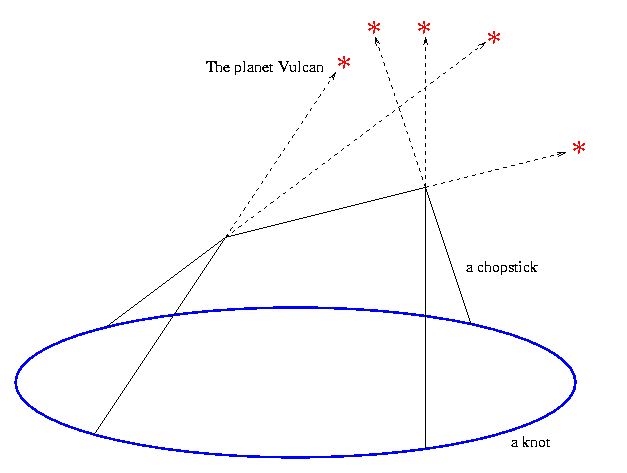
We therefore pick a knot, given as a specific embedding of S1 in R3, and count the number of "Stonehenge-inspired chopstick towers" that can be built upon it; namely, the number of delicate arrangements of chopsticks whose ends are lying on the knot or are supporting each other in trivalent corners joining three chopsticks each, so that each chopstick is pointing at a different pre chosen point in heaven that has a high mythical meaning.
Quite amazingly, when these stellar webs are counted correctly, the result is a knot invariant valued in some space of diagrams, deeply related to certain aspects of Lie theory. This allows for a rich interplay between the two seemingly unrelated topics of knots and Lie algebras. In addition, the resulting invariant has some nice universallity properties - in the appropriate sense, it a "universal polynomial invariant of knots".
While all of this could have been discovered some 4,000 years ago by any visitor to Stonehenge, the history of the subject is somewhat briefer, involving the names Witten, Vassiliev, Bott, Taubes, and D. Thurston, and mostly involving dates later than 1988.