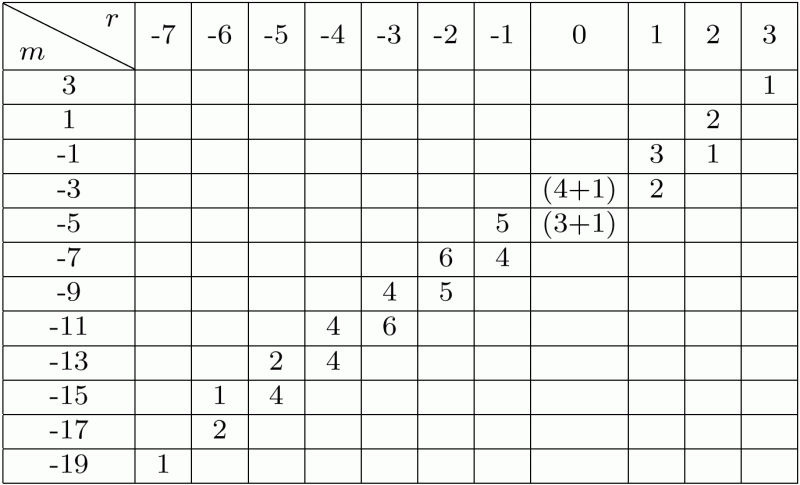
Dimensions of the rational homology of the knot 10(100) at height r and degree m
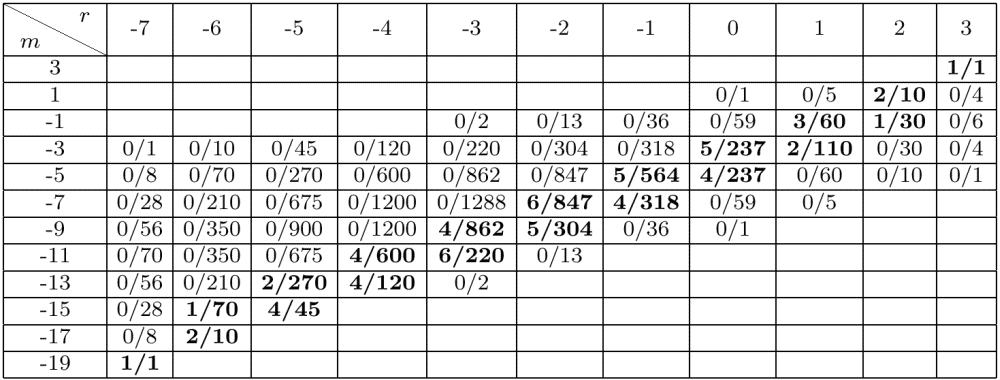
(dim homology)/(dim chains) for the knot 10(100) at height r and degree m

| Like in the case of the Jones polynomial, we don't have a topological interpretation of categorification. | ||
| Unlike the case of the Jones polynomial, we don't have a characterization of categorification, only a construction. | ||
| We don't have a "physical" explanation of categorification (like Witten's Chern-Simons explanation of many other knot invariants). | ||
| We don't know how to repeat the story in the case of other knot polynomials. | ||
| We don't know to generalize categorification to the case of knots inside other 3-manifolds. | ||
| We don't know if the story generalizes to the case of invariants of 3-manifolds. | ||
| Categorification doesn't seem to generalize to virtual knots. | ||
| We don't understand why the rational homology for all the knots for which it was computed always decomposes as a sum of many "knight moves" and a single "pawn move" at height 0. |
 Dimensions of the rational homology of the knot 10(100) at height r and degree m | |
| We know a reason why the dimensions of the rational homology are so much smaller than the dimensions of the corresponding chain spaces, but perhaps it isn't the right reason. Is there a much smaller complex that computes the same homology? Perhaps based on maximal trees in the checkerboard graph of the knot? |
 (dim homology)/(dim chains) for the knot 10(100) at height r and degree m | |

| The Thistlethwaite link, it's checkerboard coloring, it's graph, and a maximal tree in it. | |