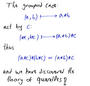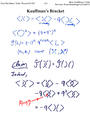© | << < ? > >> |
Dror Bar-Natan:
Talks:
The Unreasonable Affinity of Knot Theory and the Algebraic Sciences
Wayne State University Math
Colloquium, November 3 2003
In an article bearing a similar title1, Eugene Wigner once wondered about the
numerous and unexpected ways in which mathematics comes into play in
the natural sciences. While our topic and claims are much humbler, we
find ourselves puzzled by the unreasonable affinity of knot theory and
certain parts of algebra. It figures that knot theory is related to
3-dimensional topology. But why on earth should the mundane study of
tangled shoelaces and unwieldy piles of seamen's rope be related to the
elegance and sophistication of the likes of Lie algebras,
6j-symbols and homological algebra?
I'll start with the vague but fundamental relationship between knots,
quandles and Lie algebras, which in my opinion is one of the quickest
ways to notice that there's something algebraically deep about knots.
I'll wave my hands about the deep relations via quantum field theory
and quantum groups, talk a little about the Kauffman bracket and the
Jones polynomial, and say a few words about Khovanov's categorification
of the Jones polynomial2,3. That last topic is hardly understood;
perhaps because it is the one place where knot theory is a bit ahead of
its algebra.
1 Eugene Wigner, The
Unreasonable Effectiveness of Mathematics in the Natural
Sciences, Communications in Pure and Applied Mathematics
13-I (1960).
2 Mikhail Khovanov, A
categorification of the Jones polynomial, arXiv:math.QA/9908171.
3 Dror Bar-Natan, On Khovanov's
categorification of the Jones polynomial, arXiv:math.GT/0201043.