Talks
(in reverse chronological order)
Future Talks / Travel:
Mexico City (April 12-28, 2024),
Groningen (April 29 - June 16, 2024),
Beijing (July 18-31?)?,
Les Diablerets (August 5-11?, 2024),
Geneva (August 11-18?, 2024),
Sydney (May 25? - July 6?, 2025).
Highlighted Talks:
(see all talks)
 Geneva-231201: Shifted Partial Quadratics, their Pushforwards, and Signature Invariants for Tangles, University of Geneva seminar, December 2023.
Geneva-231201: Shifted Partial Quadratics, their Pushforwards, and Signature Invariants for Tangles, University of Geneva seminar, December 2023.
 Tokyo-230911: Rooting the BKT for FTI, Tokyo University seminar, September 2023.
Tokyo-230911: Rooting the BKT for FTI, Tokyo University seminar, September 2023.
 Ottawa-2306: Computing the Zombian of an Unfinished Columbarium, CMS Summer 2023 Meeting, Ottawa June 2023.
Ottawa-2306: Computing the Zombian of an Unfinished Columbarium, CMS Summer 2023 Meeting, Ottawa June 2023.
 Oaxaca-2210: Cars, Interchanges, Traffic Counters, and some Pretty Darned Good Knot Invariants, Using Quantum Invariants to do Interesting Topology, Oaxaca, October 2022.
Oaxaca-2210: Cars, Interchanges, Traffic Counters, and some Pretty Darned Good Knot Invariants, Using Quantum Invariants to do Interesting Topology, Oaxaca, October 2022.
 LesDiablerets-2208: Tangles in a Pole Dance Studio: A Reading of Massuyeau, Alekseev, and Naef, Les Disblerets, August-September 2022.
LesDiablerets-2208: Tangles in a Pole Dance Studio: A Reading of Massuyeau, Alekseev, and Naef, Les Disblerets, August-September 2022.
 CMS-2112: Kashaev's Signature Conjecture, CMS Winter 2021 Meeting, December 2021.
CMS-2112: Kashaev's Signature Conjecture, CMS Winter 2021 Meeting, December 2021.
 KOS-211021: Yarn-Ball Knots, [K-OS] seminar, October 2021.
KOS-211021: Yarn-Ball Knots, [K-OS] seminar, October 2021.
 MoscowByWeb-2104: I Still Don't Understand the Alexander Polynomial, Bauman Moscow State Technical University Mathematical Colloquium, online, April 2021.
MoscowByWeb-2104: I Still Don't Understand the Alexander Polynomial, Bauman Moscow State Technical University Mathematical Colloquium, online, April 2021.
 LearningSeminarOnCategorification-2006: The Alexander Polynomial is a Quantum Invariant in a Different Way, "Learning Seminar on Categorification", online, June 2020.
LearningSeminarOnCategorification-2006: The Alexander Polynomial is a Quantum Invariant in a Different Way, "Learning Seminar on Categorification", online, June 2020.
 TrendsInLDT-2005: Over Then Under Tangles, "Trends in Low-Dimensional Topology", online, May 2020.
TrendsInLDT-2005: Over Then Under Tangles, "Trends in Low-Dimensional Topology", online, May 2020.
 MoscowByWeb-2004: Over Then Under Tangles, "Knots and Representation Theory" seminar, Moscow (via Zoom), April 2020.
MoscowByWeb-2004: Over Then Under Tangles, "Knots and Representation Theory" seminar, Moscow (via Zoom), April 2020.
 Toronto-1912: Geography vs. Identity - and - Chord Diagrams, Knots, and Lie Algebras, CMS Winter 2019 meeting, December 2019.
Toronto-1912: Geography vs. Identity - and - Chord Diagrams, Knots, and Lie Algebras, CMS Winter 2019 meeting, December 2019.
 UCLA-191101: Some Feynman Diagrams in Algebra, UCLA Topology seminar, November 2019.
UCLA-191101: Some Feynman Diagrams in Algebra, UCLA Topology seminar, November 2019.
 Sydney-190916: Algebraic Knot Theory, Sydney Topology seminar, September 2019.
Sydney-190916: Algebraic Knot Theory, Sydney Topology seminar, September 2019.
 CRM-1907: Expansions, Lie Algebras, and Invariants, workshop in Montreal, July 2019.
CRM-1907: Expansions, Lie Algebras, and Invariants, workshop in Montreal, July 2019.
 DaNang-1905: Everything around slε2+ is DoPeGDO. So what?, Quantum Topology and Hyperbolic Geometry Conference, Da Nang, Vietnam, May 2019.
DaNang-1905: Everything around slε2+ is DoPeGDO. So what?, Quantum Topology and Hyperbolic Geometry Conference, Da Nang, Vietnam, May 2019.
 Toronto-1811: Computation without Representation, Toronto colloquium, November 2018.
Toronto-1811: Computation without Representation, Toronto colloquium, November 2018.
 MAASeaway-1810: My Favourite First-Year Analysis Theorem, MAA Seaway Section Fall 2018 Meeting, University of Toronto at Mississauga, October 2018.
MAASeaway-1810: My Favourite First-Year Analysis Theorem, MAA Seaway Section Fall 2018 Meeting, University of Toronto at Mississauga, October 2018.
 StonyBrook-1805: Computation without Representation, Simons Center for Geometry and Physics, Stony Brook, May 2018.
StonyBrook-1805: Computation without Representation, Simons Center for Geometry and Physics, Stony Brook, May 2018.
 Matemale-1804: Solvable Approximations of the Quantum sl2 Portfolio, four talks in Matemale, France, in April 2018 (along with 4 more by Roland van der Veen and 10 more by other speakers).
Matemale-1804: Solvable Approximations of the Quantum sl2 Portfolio, four talks in Matemale, France, in April 2018 (along with 4 more by Roland van der Veen and 10 more by other speakers).
 LesDiablerets-1708: The Dogma is Wrong, Lie Groups in Mathematics and Physics, Les Diablerets, August 2017.
LesDiablerets-1708: The Dogma is Wrong, Lie Groups in Mathematics and Physics, Les Diablerets, August 2017.
 McGill-1702: What else can you do with solvable approximations? McGill University HEP Seminar, February 2, 2017.
McGill-1702: What else can you do with solvable approximations? McGill University HEP Seminar, February 2, 2017.
 GWU-1612: On Elves and Invariants, Knots in Washington XLIII, George Washington University, December 2016.
GWU-1612: On Elves and Invariants, Knots in Washington XLIII, George Washington University, December 2016.
 Niagara-1612: The Hardest Math I've Ever Really Used, Public Lecture, Canadian Mathematical Society Winter Meeting, Niagara Falls, December 2016.
Niagara-1612: The Hardest Math I've Ever Really Used, Public Lecture, Canadian Mathematical Society Winter Meeting, Niagara Falls, December 2016.
 Indiana-1611: A Poly-Time Knot Polynomial Via Solvable Approximation, a two-hour talk in Indiana, November 2016.
Indiana-1611: A Poly-Time Knot Polynomial Via Solvable Approximation, a two-hour talk in Indiana, November 2016.
 LesDiablerets-1608: The Brute and the Hidden Paradise, mini-course in Les Diablerets, Switzerland, August 2016.
LesDiablerets-1608: The Brute and the Hidden Paradise, mini-course in Les Diablerets, Switzerland, August 2016.
 NCSU-1604: Gauss-Gassner Invariants, North Carolina State University, April 2016.
NCSU-1604: Gauss-Gassner Invariants, North Carolina State University, April 2016.
 Leiden-1601: The Kashiwara-Vergne Problem and Topology, Leiden, January 2016.
Leiden-1601: The Kashiwara-Vergne Problem and Topology, Leiden, January 2016.
 MoscowByWeb-1511: Crossing the Crossings, "Knots and Representation Theory" seminar, Moscow (via Skype), November 2015.
MoscowByWeb-1511: Crossing the Crossings, "Knots and Representation Theory" seminar, Moscow (via Skype), November 2015.
 Cornell-150925: Knots in Three and Four Dimensions, Kieval Lecture, Cornell University, September 2015.
Cornell-150925: Knots in Three and Four Dimensions, Kieval Lecture, Cornell University, September 2015.
 LesDiablerets-1508: Polynomial Time Knot Polynomials, Les Diablerets, Switzerland, August 2015.
LesDiablerets-1508: Polynomial Time Knot Polynomials, Les Diablerets, Switzerland, August 2015.
 Louvain-1506: Expansions, Five Chaire de la Vallée-Poussin talks in Louvain-la-Neuve, Belgium, June 1-5, 2015.
Louvain-1506: Expansions, Five Chaire de la Vallée-Poussin talks in Louvain-la-Neuve, Belgium, June 1-5, 2015.
 CMU-1504: Commutators, Carnegie Mellon University, April 2015.
CMU-1504: Commutators, Carnegie Mellon University, April 2015.
 Georgetown-1503: When does a group have a Taylor expansion? Georgetown University, March 2015.
Georgetown-1503: When does a group have a Taylor expansion? Georgetown University, March 2015.
 Hamilton-1412: Tangles, Wheels, Balloons, Hamilton, December 2014.
Hamilton-1412: Tangles, Wheels, Balloons, Hamilton, December 2014.
 Fields-1411: Talks at the "Legacy of Vladimir Arnold" Conference: Dessert: Hilbert's 13th Problem, in Full Colour and Finite Type Invariants of Doodles, The Fields Institute, November 2014.
Fields-1411: Talks at the "Legacy of Vladimir Arnold" Conference: Dessert: Hilbert's 13th Problem, in Full Colour and Finite Type Invariants of Doodles, The Fields Institute, November 2014.
 Treehouse-1410: The 17 Tiling Patterns: Gotta Catch 'Em All!, Treehouse Talks, October 2014.
Treehouse-1410: The 17 Tiling Patterns: Gotta Catch 'Em All!, Treehouse Talks, October 2014.
 ClassroomAdventures-1408: The 17 Worlds of Planar Ants, Classroom Adventures in Mathematics, Toronto, August 2014.
ClassroomAdventures-1408: The 17 Worlds of Planar Ants, Classroom Adventures in Mathematics, Toronto, August 2014.
 Oberwolfach-1405: Some very good formulas for the Alexander polynomial Oberwolfach, May 2014.
Oberwolfach-1405: Some very good formulas for the Alexander polynomial Oberwolfach, May 2014.
 Vienna-1402: A Partial Reduction of BF Theory to Combinatorics, Vienna, February 2014.
Vienna-1402: A Partial Reduction of BF Theory to Combinatorics, Vienna, February 2014.
 ClassroomAdventures-1401: Visualizing the Fourth Dimension, and the Simplest Thing I Don't Know About It, Classroom Adventures in Mathematics, Toronto, January 2014.
ClassroomAdventures-1401: Visualizing the Fourth Dimension, and the Simplest Thing I Don't Know About It, Classroom Adventures in Mathematics, Toronto, January 2014.
- HUJI-140101: קשרים בארבעה מימדים והבעיה הפתוחה הפשוטה ביותר אודותם, (Knots in Four Dimensions and the Simplest Open Problem About Them, Hebrew lecture), Jerusalem, January 2014.
 Zurich-1310: Informal Talks on the Topology, Combinatorics, and Low and High Algebra of w-Knots, 6 talks in Zurich, October 2013.
Zurich-1310: Informal Talks on the Topology, Combinatorics, and Low and High Algebra of w-Knots, 6 talks in Zurich, October 2013.
 Geneva-131024: Finite Type Invariants of Ribbon Knotted Balloons and Hoops, Geneva, October 2013.
Geneva-131024: Finite Type Invariants of Ribbon Knotted Balloons and Hoops, Geneva, October 2013.
 Geneva-130917: Trees and Wheels and Balloons and Hoops and More Later, Geneva, September 2013.
Geneva-130917: Trees and Wheels and Balloons and Hoops and More Later, Geneva, September 2013.
 ClassroomAdventures-1308: On Maps, Machines and Roaches, Classroom Adventures in Mathematics, August 2013.
ClassroomAdventures-1308: On Maps, Machines and Roaches, Classroom Adventures in Mathematics, August 2013.
 Montreal-1306: A Quick Introduction to Khovanov Homology, two talks in Montreal, June 2013 (plus one more on meta-groups).
Montreal-1306: A Quick Introduction to Khovanov Homology, two talks in Montreal, June 2013 (plus one more on meta-groups).
 Aarhus-1305: (u, v, and w knots) x (topology, combinatorics, low algebra,
and high algebra), QGM Master Class, Aarhus May-June 2013.
Aarhus-1305: (u, v, and w knots) x (topology, combinatorics, low algebra,
and high algebra), QGM Master Class, Aarhus May-June 2013.
 Cambridge-1301: Non-Commutative Gaussian Elimination and Rubik's Cube,
Cambridge, January 2013.
Cambridge-1301: Non-Commutative Gaussian Elimination and Rubik's Cube,
Cambridge, January 2013.
 Newton-1301: Braids and the Grothendieck-Teichmuller Group, and
Meta-Groups, Meta-Bicrossed-Products, and the Alexander
Polynomial,the Newton Institute, January 2011.
Newton-1301: Braids and the Grothendieck-Teichmuller Group, and
Meta-Groups, Meta-Bicrossed-Products, and the Alexander
Polynomial,the Newton Institute, January 2011.
 Hamburg-1208: A Quick Introduction to Khovanov Homology and Balloons
and Hoops and their Universal Finite Type Invariant, BF Theory, and an
Ultimate Alexander Invariant, two talks in Hamburg, August 2012.
Hamburg-1208: A Quick Introduction to Khovanov Homology and Balloons
and Hoops and their Universal Finite Type Invariant, BF Theory, and an
Ultimate Alexander Invariant, two talks in Hamburg, August 2012.
 Caen-1206: Caen Workshop on v- and w-Knotted Objects, about 25 hours
of talks over 9 days in June 2012 in Caen, France.
Caen-1206: Caen Workshop on v- and w-Knotted Objects, about 25 hours
of talks over 9 days in June 2012 in Caen, France.
- Oregon-1108: The Pure Virtual Braid Group is Quadratic, Oregon, August
2011.
 SwissKnots-1105: Facts and Dreams About v-Knots and Etingof-Kazhdan, Swiss
Knots 2011, Lake Thun, May 2011.
SwissKnots-1105: Facts and Dreams About v-Knots and Etingof-Kazhdan, Swiss
Knots 2011, Lake Thun, May 2011.
 Tennessee-1103: Cosmic Coincidences and Several Other Stories, Tennnessee,
March 2011.
Tennessee-1103: Cosmic Coincidences and Several Other Stories, Tennnessee,
March 2011.
 Chicago-1009: From the ax+b Lie Algebra to the Alexander
Polynomial and Beyond, and 18 Conjectures, Chicago, September
2010.
Chicago-1009: From the ax+b Lie Algebra to the Alexander
Polynomial and Beyond, and 18 Conjectures, Chicago, September
2010.
 Montpellier-1006: I understand Drinfel'd and Alekseev-Torossian, I don't
understand Etingof-Kazhdan yet, and I'm clueless about Kontsevich,
three talks in Montpellier, June 2010.
Montpellier-1006: I understand Drinfel'd and Alekseev-Torossian, I don't
understand Etingof-Kazhdan yet, and I'm clueless about Kontsevich,
three talks in Montpellier, June 2010.
 Goettingen-1004: u, v, and w-Knots: Topology, Combinatorics and Low and High
Algebra, Courant Lecture Series, Goettingen, April 2010.
Goettingen-1004: u, v, and w-Knots: Topology, Combinatorics and Low and High
Algebra, Courant Lecture Series, Goettingen, April 2010.
 Bonn-0908: Convolutions on Lie Groups and Lie Algebras and Ribbon
2-Knots, Bonn, August 2009.
Bonn-0908: Convolutions on Lie Groups and Lie Algebras and Ribbon
2-Knots, Bonn, August 2009.
- Trieste-0905: (u, v, and w knots) x (topology, combinatorics, low algebra,
and high algebra), Trieste, May 2009.
- Sandbjerg-0810: The Penultimate Alexander Invariant, Sandbjerg, Denmark, October 2008.
 MSRI-0808: Projectivization, W-Knots, Kashiwara-Vergne and Alekseev-Torossian, MSRI, August 2008.
MSRI-0808: Projectivization, W-Knots, Kashiwara-Vergne and Alekseev-Torossian, MSRI, August 2008.
- Fields-0709: A Very Non-Planar Very Planar Algebra, The Fields Institute, September 2007.
- Hanoi-0708: Following Lin: Expansions for Groups, Vietnamese Academy of Science and Technology, August 2007.
 Aarhus-0706: Algebraic Knot Theory, Århus University, June 2007.
Aarhus-0706: Algebraic Knot Theory, Århus University, June 2007.
- Kyoto-0705: The Virtues of Being an Isomorphism, RIMS, Kyoto May 2007.
- UofT-GS-070308: A Homological Construction of the Exponential Function, Graduate Student Seminar, University of Toronto, January 2005.
- Utah-0506: Local Khovanov Homology - Computations and Mutations,
Snowbird, Utah, June 2005
- UIUC-050311: I don't understand Khovanov-Rozansky homology, University
of Illinois at Urbana-Champaign, March 2005.
- GWU-050213: I've Computed Kh(T(9,5)) and I'm Happy, George Washington
University, February 2005.
- UofT-GS-050113: Gödel's Incompleteness Theorem, Graduate Student
Seminar, University of Toronto, January 2005.
- UWO-040213: Probability: Fact, Fiction and Quantum and Khovanov
Homology for Knots and Links, University of Western Ontario,
February 2004.
- UofT-040205: "Not Knot" and "Outside In", University of Toronto,
February 2004.
- BIRS-0311: Introduction to Perturbative Chern-Simons Theory and
Introduction to Khovanov Homology, BIRS, Banff, November 2003.
- Wayne-031103: The Unreasonable Affinity of Knot Theory and the Algebraic
Sciences, Wayne State University, November 2003.
- Davis-010813: Algebraic Structures on Spaces of Knots, University of
California at Davis, August 2001.
- HUJI-010118:
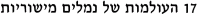 ,
The Hebrew University, January 2001.
,
The Hebrew University, January 2001.
- Fields-010111: Knot Invariants, Associators and a Strange Breed of Planar
Algebras, The Fields Institute, January 2001.
 MSRI-001206: Finite type invariants and a strange breed of planar
algebras, MSRI December 2000.
MSRI-001206: Finite type invariants and a strange breed of planar
algebras, MSRI December 2000.
 CUNY-001205: On Links, Functions, Integrals and 3-Manifold Invariants, Einstein Chair Mathematics Seminar, CUNY, December 2000.
CUNY-001205: On Links, Functions, Integrals and 3-Manifold Invariants, Einstein Chair Mathematics Seminar, CUNY, December 2000.
- UCB-000215: Embedded Trivalent Graphs and an Infant Conjecture,
Berkeley, February 2000.
- JHU-991027: The Harish-Chandra-Duflo Isomorphism is as Easy as 1+1=2,
Johns Hopkins University, October 1999.
- Srni-9901: From Astrology to Topology via Feynman Diagrams and Lie
Algebras, Srni, January 1999.
Talks Since November 1998:
(259 listed, 83 highlighted).
Indiana-2402,
USC-240205,
McMaster-240118,
 Geneva-231201,
Geneva-231201,
 Budapest-2311,
Waterloo-231030,
Budapest-2311,
Waterloo-231030,
 Tokyo-230911,
Tokyo-230911,
Waseda-2309,
Waseda-2308,
Nara-2308,
Tokyo-230808,
Kyoto-230727,
 Ottawa-2306,
Ottawa-2306,
 ICERM-2305,
Sydney-230327,
ICERM-2305,
Sydney-230327,
 CMS-2212,
UCLA-221104,
CMS-2212,
UCLA-221104,
 Oaxaca-2210,
Oaxaca-2210,
 LesDiablerets-2208,
LesDiablerets-2208,
 Geneva-2206,
Groningen-220620,
ICERM-220422,
Geneva-2206,
Groningen-220620,
ICERM-220422,
 Waco-2203,
Waco-2203,
 CMS-2112,
CMS-2112,
 KOS-211021,
MathCamp-2107,
KOS-211021,
MathCamp-2107,
 SyracuseByWeb-2104,
SyracuseByWeb-2104,
 MoscowByWeb-2104,
MoscowByWeb-2104,
 Fields-2011,
Fields-2011,
 CUMC-200820,
CUMC-200820,
 LearningSeminarOnCategorification-2006,
LearningSeminarOnCategorification-2006,
 MathUnion-200604,
MathUnion-200604,
 TrendsInLDT-2005,
TrendsInLDT-2005,
 MoscowByWeb-2004,
Groningen-2002,
Bonn-200120,
HUJI-1912,
MoscowByWeb-2004,
Groningen-2002,
Bonn-200120,
HUJI-1912,
 Toronto-1912,
Columbia-191125,
Toronto-1912,
Columbia-191125,
Banff-1911,
 UCLA-191101,
Macquarie-191023,
Macquarie-191016,
Monash-191009,
Melbourne-191007,
UCLA-191101,
Macquarie-191023,
Macquarie-191016,
Monash-191009,
Melbourne-191007,
 Sydney-191002,
Canberra-190927,
Sydney-191002,
Canberra-190927,
 Sydney-190916,
Sydney-190912,
QMUL-1908,
Sydney-190916,
Sydney-190912,
QMUL-1908,
 CRM-1907,
CRM-1907,
 DaNang-1905,
Indiana-1902,
Ohio-1901,
DaNang-1905,
Indiana-1902,
Ohio-1901,
 Toronto-1811,
Toronto-1811,
 Hefei-1811,
Hefei-1811,
 MAASeaway-1810,
McMaster-180921,
MAASeaway-1810,
McMaster-180921,
 BonnByWeb-1805,
BonnByWeb-1805,
 StonyBrook-1805,
StonyBrook-1805,
 Matemale-1804,
Perimeter-180312,
Buffalo-170916,
Matemale-1804,
Perimeter-180312,
Buffalo-170916,
 LesDiablerets-1708,
LesDiablerets-1708,
 Sydney-1708,
Sydney-1708,
 Toulouse-1705,
Toulouse-1705,
 McGill-1702,
McGill-1702,
 GWU-1612,
GWU-1612,
 MIT-1612,
MIT-1612,
 Niagara-1612,
Niagara-1612,
 Indiana-1611,
Indiana-1611,
 UNC-1610,
UNC-1610,
 Toronto-1609,
Toronto-1609,
 LesDiablerets-1608,
LesDiablerets-1608,
 Greece-1607,
SciRen-1605,
Greece-1607,
SciRen-1605,
 NCSU-1604,
NCSU-1604,
 Iowa-1603,
Northeastern-1602,
Iowa-1603,
Northeastern-1602,
 Leiden-1601,
Leiden-1601,
 MoscowByWeb-1511,
MUGS-1510,
Loyola-1510,
MoscowByWeb-1511,
MUGS-1510,
Loyola-1510,
 Cornell-150925,
Cornell-150925,
 LesDiablerets-1508,
LesDiablerets-1508,
 Aarhus-1507,
Qinhuangdao-1507,
Aarhus-1507,
Qinhuangdao-1507,
 Louvain-1506,
Toronto-150514,
Louvain-1506,
Toronto-150514,
 CMU-1504,
CMU-1504,
 Georgetown-1503,
TCDSB-150213,
Georgetown-1503,
TCDSB-150213,
 MUGS-1501,
MUGS-1501,
 Hamilton-1412,
Hamilton-1412,
 Fields-1411,
Fields-1411,
 Treehouse-1410,
Treehouse-1410,
 ClassroomAdventures-1408,
CanadaMathCamp-1407,
ClassroomAdventures-1408,
CanadaMathCamp-1407,
 Bannoye-1407,
Bannoye-1407,
 Oberwolfach-1405,
Oberwolfach-1405,
 Vienna-1402,
McMaster-140130,
Vienna-1402,
McMaster-140130,
 ClassroomAdventures-1401,
HUJI-140101,
Grenoble-1311,
Lausanne-131118,
ClassroomAdventures-1401,
HUJI-140101,
Grenoble-1311,
Lausanne-131118,
 Bern-131104,
Bern-131104,
 Zurich-1310,
Zurich-1310,
 Geneva-131024,
Geneva-131024,
 Geneva-131008,
Geneva-131008,
 Zurich-130919,
Zurich-130919,
 Geneva-130917,
Geneva-130917,
 ClassroomAdventures-1308,
CanadaMathCamp-1308,
ClassroomAdventures-1308,
CanadaMathCamp-1308,
 CUMC-1307,
CUMC-1307,
 Montreal-1306,
Montreal-1306,
 Aarhus-1305,
Singapore-1305,
Aarhus-1305,
Singapore-1305,
 NhaTrang-1305,
NhaTrang-1305,
 Chicago-1303,
Chicago-1303,
 Toronto-1303,
Sheffield-130206,
Toronto-1303,
Sheffield-130206,
 Cambridge-1301,
Cambridge-1301,
 Oxford-130121,
Imperial-130118,
Oxford-130121,
Imperial-130118,
 Newton-1301,
Israel-1301,
MtAllison-121013,
Newton-1301,
Israel-1301,
MtAllison-121013,
 Hamburg-1208,
Hamburg-1208,
 CanadaMathCamp-1208,
CanadaMathCamp-1208,
 Caen-1206,
Caen-1206,
 Regina-1206,
Regina-1206,
 Binghamton-1203,
Binghamton-1203,
 GWU-1203,
GWU-1203,
 Buffalo-1203,
CanadianPerspectives-1110,
StBonaventure-1110,
Buffalo-1203,
CanadianPerspectives-1110,
StBonaventure-1110,
 Strasbourg-1109,
Oregon-1108,
Strasbourg-1109,
Oregon-1108,
 Colombia-1107,
Geneva-110531,
Colombia-1107,
Geneva-110531,
 SwissKnots-1105,
SwissKnots-1105,
 Tennessee-1103,
Tennessee-1103,
 RCI-110213,
RCI-110213,
 Toronto-110110,
Toronto-110110,
 Chicago-1009,
Chicago-1009,
 Montpellier-1006,
Montpellier-1006,
 Toronto-1005,
Toronto-1005,
 Goettingen-1004,
Goettingen-1004,
Luminy-1004,
 UWO-100225,
UWO-100225,
 Fields-0911,
UofT-GS-090930,
Fields-0911,
UofT-GS-090930,
 Bonn-0908,
Bonn-0908,
 HUJI-090727,
HUJI-090727,
 Mathcamp-0907,
Paris-0906,
Trieste-0905,
KSU-090407,
Bogota-0902,
PSU-090205,
Northeastern-081028,
Copenhagen-081009,
Sandbjerg-0810,
Mathcamp-0907,
Paris-0906,
Trieste-0905,
KSU-090407,
Bogota-0902,
PSU-090205,
Northeastern-081028,
Copenhagen-081009,
Sandbjerg-0810,
 MSRI-0808,
CUMC-0807,
Geneva-0805,
Zurich-080513,
Oberwolfach-0805,
Brown-071114,
UofT-GS-071023,
Fields-0709,
Hanoi-0708,
Tianjin-0707,
MSRI-0808,
CUMC-0807,
Geneva-0805,
Zurich-080513,
Oberwolfach-0805,
Brown-071114,
UofT-GS-071023,
Fields-0709,
Hanoi-0708,
Tianjin-0707,
 Aarhus-0706,
Kyoto-0705,
TiTech-070508,
Buffalo-070323,
UofT-GS-070308,
Columbia-070209,
HUJI-061228,
Uppsala-0609,
UofT-0608,
Istanbul-0606,
Iowa-060120,
HUJI-060101,
GaTech-051021,
UofT-051014,
UQAM-051001,
Oberwolfach-0506,
Utah-0506,
Amsterdam-050418,
LSU-0504,
UIUC-050311,
GiftedConference-050215,
GWU-050213,
MASSU-050119,
UofT-GS-050113,
UofT-041208,
York-041108,
Harvard-0410,
Buffalo-0410,
Oporto-0407,
GWU-0405,
Microsoft-040413,
Rochester-040402,
MSU-0402,
UWO-040213,
UofT-040205,
Queens-040123,
UofT-031208,
BIRS-0311,
Wayne-031103,
UofT-031002,
UIC-030905,
Warsaw-030711,
Potsdam-030604,
Cornell-030501,
Harvard-030418,
UofT-030331,
Columbia-030328,
JHU-0303,
UNC-0302,
HUJI-021230,
BU-021101,
UofT-021010,
McMaster-021005,
UQAM-020927,
HUJI-020613,
BIU-020320,
Toronto-0202,
Toronto-020211,
HUJI-011104,
Kyoto-0109,
Calgary-010824,
Davis-010813,
HUJI-010118,
Fields-010111,
Aarhus-0706,
Kyoto-0705,
TiTech-070508,
Buffalo-070323,
UofT-GS-070308,
Columbia-070209,
HUJI-061228,
Uppsala-0609,
UofT-0608,
Istanbul-0606,
Iowa-060120,
HUJI-060101,
GaTech-051021,
UofT-051014,
UQAM-051001,
Oberwolfach-0506,
Utah-0506,
Amsterdam-050418,
LSU-0504,
UIUC-050311,
GiftedConference-050215,
GWU-050213,
MASSU-050119,
UofT-GS-050113,
UofT-041208,
York-041108,
Harvard-0410,
Buffalo-0410,
Oporto-0407,
GWU-0405,
Microsoft-040413,
Rochester-040402,
MSU-0402,
UWO-040213,
UofT-040205,
Queens-040123,
UofT-031208,
BIRS-0311,
Wayne-031103,
UofT-031002,
UIC-030905,
Warsaw-030711,
Potsdam-030604,
Cornell-030501,
Harvard-030418,
UofT-030331,
Columbia-030328,
JHU-0303,
UNC-0302,
HUJI-021230,
BU-021101,
UofT-021010,
McMaster-021005,
UQAM-020927,
HUJI-020613,
BIU-020320,
Toronto-0202,
Toronto-020211,
HUJI-011104,
Kyoto-0109,
Calgary-010824,
Davis-010813,
HUJI-010118,
Fields-010111,
 MSRI-001206,
MSRI-001206,
 CUNY-001205,
HUJI-001116,
Compugen-001101,
Lehigh-0006,
Riverside-000429,
UCB-0004,
UCB-000420,
CalTech-000221,
UCB-000215,
UCSD-000113,
GaTech-991203,
UMD-991029,
JHU-991027,
UCB-9910,
UCB-990915,
Srni-9901,
HUJI-981203,
Aarhus-9811-2,
Aarhus-9811-1,
BGU-981103
CUNY-001205,
HUJI-001116,
Compugen-001101,
Lehigh-0006,
Riverside-000429,
UCB-0004,
UCB-000420,
CalTech-000221,
UCB-000215,
UCSD-000113,
GaTech-991203,
UMD-991029,
JHU-991027,
UCB-9910,
UCB-990915,
Srni-9901,
HUJI-981203,
Aarhus-9811-2,
Aarhus-9811-1,
BGU-981103
On first inspection, in their jars, or aquariums, or ouroboriums,
they appear to be simply domesticated serpents, writhing as they do
suspended in the ether. But of course, there's more to mythological
creatures, even domesticated varieties, than meets the eye. Know this
about the ouroborus: when one chooses to bite its own tail - a choice
which sooner or later every one of its kind is destined to make - it
cannot release it. It will spend the rest of its existence as a
never-ending loop. It might twist and writhe and flatten and flex,
but it is forever hooped.
An
ouroborus in a jar on the shelf, from the Planetarium.
 Geneva-231201: Shifted Partial Quadratics, their Pushforwards, and Signature Invariants for Tangles, University of Geneva seminar, December 2023.
Geneva-231201: Shifted Partial Quadratics, their Pushforwards, and Signature Invariants for Tangles, University of Geneva seminar, December 2023.
 Tokyo-230911: Rooting the BKT for FTI, Tokyo University seminar, September 2023.
Tokyo-230911: Rooting the BKT for FTI, Tokyo University seminar, September 2023.
 Ottawa-2306: Computing the Zombian of an Unfinished Columbarium, CMS Summer 2023 Meeting, Ottawa June 2023.
Ottawa-2306: Computing the Zombian of an Unfinished Columbarium, CMS Summer 2023 Meeting, Ottawa June 2023.
 Oaxaca-2210: Cars, Interchanges, Traffic Counters, and some Pretty Darned Good Knot Invariants, Using Quantum Invariants to do Interesting Topology, Oaxaca, October 2022.
Oaxaca-2210: Cars, Interchanges, Traffic Counters, and some Pretty Darned Good Knot Invariants, Using Quantum Invariants to do Interesting Topology, Oaxaca, October 2022.
 LesDiablerets-2208: Tangles in a Pole Dance Studio: A Reading of Massuyeau, Alekseev, and Naef, Les Disblerets, August-September 2022.
LesDiablerets-2208: Tangles in a Pole Dance Studio: A Reading of Massuyeau, Alekseev, and Naef, Les Disblerets, August-September 2022.
 CMS-2112: Kashaev's Signature Conjecture, CMS Winter 2021 Meeting, December 2021.
CMS-2112: Kashaev's Signature Conjecture, CMS Winter 2021 Meeting, December 2021.
 KOS-211021: Yarn-Ball Knots, [K-OS] seminar, October 2021.
KOS-211021: Yarn-Ball Knots, [K-OS] seminar, October 2021.
 MoscowByWeb-2104: I Still Don't Understand the Alexander Polynomial, Bauman Moscow State Technical University Mathematical Colloquium, online, April 2021.
MoscowByWeb-2104: I Still Don't Understand the Alexander Polynomial, Bauman Moscow State Technical University Mathematical Colloquium, online, April 2021.
 LearningSeminarOnCategorification-2006: The Alexander Polynomial is a Quantum Invariant in a Different Way, "Learning Seminar on Categorification", online, June 2020.
LearningSeminarOnCategorification-2006: The Alexander Polynomial is a Quantum Invariant in a Different Way, "Learning Seminar on Categorification", online, June 2020.
 TrendsInLDT-2005: Over Then Under Tangles, "Trends in Low-Dimensional Topology", online, May 2020.
TrendsInLDT-2005: Over Then Under Tangles, "Trends in Low-Dimensional Topology", online, May 2020.
 MoscowByWeb-2004: Over Then Under Tangles, "Knots and Representation Theory" seminar, Moscow (via Zoom), April 2020.
MoscowByWeb-2004: Over Then Under Tangles, "Knots and Representation Theory" seminar, Moscow (via Zoom), April 2020.
 Toronto-1912: Geography vs. Identity - and - Chord Diagrams, Knots, and Lie Algebras, CMS Winter 2019 meeting, December 2019.
Toronto-1912: Geography vs. Identity - and - Chord Diagrams, Knots, and Lie Algebras, CMS Winter 2019 meeting, December 2019.
 UCLA-191101: Some Feynman Diagrams in Algebra, UCLA Topology seminar, November 2019.
UCLA-191101: Some Feynman Diagrams in Algebra, UCLA Topology seminar, November 2019.
 Sydney-190916: Algebraic Knot Theory, Sydney Topology seminar, September 2019.
Sydney-190916: Algebraic Knot Theory, Sydney Topology seminar, September 2019.
 CRM-1907: Expansions, Lie Algebras, and Invariants, workshop in Montreal, July 2019.
CRM-1907: Expansions, Lie Algebras, and Invariants, workshop in Montreal, July 2019.
 DaNang-1905: Everything around
DaNang-1905: Everything around  Toronto-1811: Computation without Representation, Toronto colloquium, November 2018.
Toronto-1811: Computation without Representation, Toronto colloquium, November 2018.
 MAASeaway-1810: My Favourite First-Year Analysis Theorem, MAA Seaway Section Fall 2018 Meeting, University of Toronto at Mississauga, October 2018.
MAASeaway-1810: My Favourite First-Year Analysis Theorem, MAA Seaway Section Fall 2018 Meeting, University of Toronto at Mississauga, October 2018.
 StonyBrook-1805: Computation without Representation, Simons Center for Geometry and Physics, Stony Brook, May 2018.
StonyBrook-1805: Computation without Representation, Simons Center for Geometry and Physics, Stony Brook, May 2018.
 Matemale-1804: Solvable Approximations of the Quantum sl2 Portfolio, four talks in Matemale, France, in April 2018 (along with 4 more by Roland van der Veen and 10 more by other speakers).
Matemale-1804: Solvable Approximations of the Quantum sl2 Portfolio, four talks in Matemale, France, in April 2018 (along with 4 more by Roland van der Veen and 10 more by other speakers).
 LesDiablerets-1708: The Dogma is Wrong, Lie Groups in Mathematics and Physics, Les Diablerets, August 2017.
LesDiablerets-1708: The Dogma is Wrong, Lie Groups in Mathematics and Physics, Les Diablerets, August 2017.
 McGill-1702: What else can you do with solvable approximations? McGill University HEP Seminar, February 2, 2017.
McGill-1702: What else can you do with solvable approximations? McGill University HEP Seminar, February 2, 2017.
 GWU-1612: On Elves and Invariants, Knots in Washington XLIII, George Washington University, December 2016.
GWU-1612: On Elves and Invariants, Knots in Washington XLIII, George Washington University, December 2016.
 Niagara-1612: The Hardest Math I've Ever Really Used, Public Lecture, Canadian Mathematical Society Winter Meeting, Niagara Falls, December 2016.
Niagara-1612: The Hardest Math I've Ever Really Used, Public Lecture, Canadian Mathematical Society Winter Meeting, Niagara Falls, December 2016.
 Indiana-1611: A Poly-Time Knot Polynomial Via Solvable Approximation, a two-hour talk in Indiana, November 2016.
Indiana-1611: A Poly-Time Knot Polynomial Via Solvable Approximation, a two-hour talk in Indiana, November 2016.
 LesDiablerets-1608: The Brute and the Hidden Paradise, mini-course in Les Diablerets, Switzerland, August 2016.
LesDiablerets-1608: The Brute and the Hidden Paradise, mini-course in Les Diablerets, Switzerland, August 2016.
 NCSU-1604: Gauss-Gassner Invariants, North Carolina State University, April 2016.
NCSU-1604: Gauss-Gassner Invariants, North Carolina State University, April 2016.
 Leiden-1601: The Kashiwara-Vergne Problem and Topology, Leiden, January 2016.
Leiden-1601: The Kashiwara-Vergne Problem and Topology, Leiden, January 2016.
 MoscowByWeb-1511: Crossing the Crossings, "Knots and Representation Theory" seminar, Moscow (via Skype), November 2015.
MoscowByWeb-1511: Crossing the Crossings, "Knots and Representation Theory" seminar, Moscow (via Skype), November 2015.
 Cornell-150925: Knots in Three and Four Dimensions, Kieval Lecture, Cornell University, September 2015.
Cornell-150925: Knots in Three and Four Dimensions, Kieval Lecture, Cornell University, September 2015.
 LesDiablerets-1508: Polynomial Time Knot Polynomials, Les Diablerets, Switzerland, August 2015.
LesDiablerets-1508: Polynomial Time Knot Polynomials, Les Diablerets, Switzerland, August 2015.
 Louvain-1506: Expansions, Five Chaire de la Vallée-Poussin talks in Louvain-la-Neuve, Belgium, June 1-5, 2015.
Louvain-1506: Expansions, Five Chaire de la Vallée-Poussin talks in Louvain-la-Neuve, Belgium, June 1-5, 2015.
 CMU-1504: Commutators, Carnegie Mellon University, April 2015.
CMU-1504: Commutators, Carnegie Mellon University, April 2015.
 Georgetown-1503: When does a group have a Taylor expansion? Georgetown University, March 2015.
Georgetown-1503: When does a group have a Taylor expansion? Georgetown University, March 2015.
 Hamilton-1412: Tangles, Wheels, Balloons, Hamilton, December 2014.
Hamilton-1412: Tangles, Wheels, Balloons, Hamilton, December 2014.
 Fields-1411: Talks at the "Legacy of Vladimir Arnold" Conference: Dessert: Hilbert's 13th Problem, in Full Colour and Finite Type Invariants of Doodles, The Fields Institute, November 2014.
Fields-1411: Talks at the "Legacy of Vladimir Arnold" Conference: Dessert: Hilbert's 13th Problem, in Full Colour and Finite Type Invariants of Doodles, The Fields Institute, November 2014.
 Treehouse-1410: The 17 Tiling Patterns: Gotta Catch 'Em All!, Treehouse Talks, October 2014.
Treehouse-1410: The 17 Tiling Patterns: Gotta Catch 'Em All!, Treehouse Talks, October 2014.
 ClassroomAdventures-1408: The 17 Worlds of Planar Ants, Classroom Adventures in Mathematics, Toronto, August 2014.
ClassroomAdventures-1408: The 17 Worlds of Planar Ants, Classroom Adventures in Mathematics, Toronto, August 2014.
 Oberwolfach-1405: Some very good formulas for the Alexander polynomial Oberwolfach, May 2014.
Oberwolfach-1405: Some very good formulas for the Alexander polynomial Oberwolfach, May 2014.
 Vienna-1402: A Partial Reduction of BF Theory to Combinatorics, Vienna, February 2014.
Vienna-1402: A Partial Reduction of BF Theory to Combinatorics, Vienna, February 2014.
 ClassroomAdventures-1401: Visualizing the Fourth Dimension, and the Simplest Thing I Don't Know About It, Classroom Adventures in Mathematics, Toronto, January 2014.
ClassroomAdventures-1401: Visualizing the Fourth Dimension, and the Simplest Thing I Don't Know About It, Classroom Adventures in Mathematics, Toronto, January 2014.
 Zurich-1310: Informal Talks on the Topology, Combinatorics, and Low and High Algebra of w-Knots, 6 talks in Zurich, October 2013.
Zurich-1310: Informal Talks on the Topology, Combinatorics, and Low and High Algebra of w-Knots, 6 talks in Zurich, October 2013.
 Geneva-131024: Finite Type Invariants of Ribbon Knotted Balloons and Hoops, Geneva, October 2013.
Geneva-131024: Finite Type Invariants of Ribbon Knotted Balloons and Hoops, Geneva, October 2013.
 Geneva-130917: Trees and Wheels and Balloons and Hoops and More Later, Geneva, September 2013.
Geneva-130917: Trees and Wheels and Balloons and Hoops and More Later, Geneva, September 2013.
 ClassroomAdventures-1308: On Maps, Machines and Roaches, Classroom Adventures in Mathematics, August 2013.
ClassroomAdventures-1308: On Maps, Machines and Roaches, Classroom Adventures in Mathematics, August 2013.
 Montreal-1306: A Quick Introduction to Khovanov Homology, two talks in Montreal, June 2013 (plus one more on meta-groups).
Montreal-1306: A Quick Introduction to Khovanov Homology, two talks in Montreal, June 2013 (plus one more on meta-groups).
 Aarhus-1305: (u, v, and w knots) x (topology, combinatorics, low algebra,
and high algebra), QGM Master Class, Aarhus May-June 2013.
Aarhus-1305: (u, v, and w knots) x (topology, combinatorics, low algebra,
and high algebra), QGM Master Class, Aarhus May-June 2013.
 Cambridge-1301: Non-Commutative Gaussian Elimination and Rubik's Cube,
Cambridge, January 2013.
Cambridge-1301: Non-Commutative Gaussian Elimination and Rubik's Cube,
Cambridge, January 2013.
 Newton-1301: Braids and the Grothendieck-Teichmuller Group, and
Meta-Groups, Meta-Bicrossed-Products, and the Alexander
Polynomial,the Newton Institute, January 2011.
Newton-1301: Braids and the Grothendieck-Teichmuller Group, and
Meta-Groups, Meta-Bicrossed-Products, and the Alexander
Polynomial,the Newton Institute, January 2011.
 Hamburg-1208: A Quick Introduction to Khovanov Homology and Balloons
and Hoops and their Universal Finite Type Invariant, BF Theory, and an
Ultimate Alexander Invariant, two talks in Hamburg, August 2012.
Hamburg-1208: A Quick Introduction to Khovanov Homology and Balloons
and Hoops and their Universal Finite Type Invariant, BF Theory, and an
Ultimate Alexander Invariant, two talks in Hamburg, August 2012.
 Caen-1206: Caen Workshop on v- and w-Knotted Objects, about 25 hours
of talks over 9 days in June 2012 in Caen, France.
Caen-1206: Caen Workshop on v- and w-Knotted Objects, about 25 hours
of talks over 9 days in June 2012 in Caen, France.
 SwissKnots-1105: Facts and Dreams About v-Knots and Etingof-Kazhdan, Swiss
Knots 2011, Lake Thun, May 2011.
SwissKnots-1105: Facts and Dreams About v-Knots and Etingof-Kazhdan, Swiss
Knots 2011, Lake Thun, May 2011.
 Tennessee-1103: Cosmic Coincidences and Several Other Stories, Tennnessee,
March 2011.
Tennessee-1103: Cosmic Coincidences and Several Other Stories, Tennnessee,
March 2011.
 Chicago-1009: From the ax+b Lie Algebra to the Alexander
Polynomial and Beyond, and 18 Conjectures, Chicago, September
2010.
Chicago-1009: From the ax+b Lie Algebra to the Alexander
Polynomial and Beyond, and 18 Conjectures, Chicago, September
2010.
 Montpellier-1006: I understand Drinfel'd and Alekseev-Torossian, I don't
understand Etingof-Kazhdan yet, and I'm clueless about Kontsevich,
three talks in Montpellier, June 2010.
Montpellier-1006: I understand Drinfel'd and Alekseev-Torossian, I don't
understand Etingof-Kazhdan yet, and I'm clueless about Kontsevich,
three talks in Montpellier, June 2010.
 Goettingen-1004: u, v, and w-Knots: Topology, Combinatorics and Low and High
Algebra, Courant Lecture Series, Goettingen, April 2010.
Goettingen-1004: u, v, and w-Knots: Topology, Combinatorics and Low and High
Algebra, Courant Lecture Series, Goettingen, April 2010.
 Bonn-0908: Convolutions on Lie Groups and Lie Algebras and Ribbon
2-Knots, Bonn, August 2009.
Bonn-0908: Convolutions on Lie Groups and Lie Algebras and Ribbon
2-Knots, Bonn, August 2009.
 MSRI-0808: Projectivization, W-Knots, Kashiwara-Vergne and Alekseev-Torossian, MSRI, August 2008.
MSRI-0808: Projectivization, W-Knots, Kashiwara-Vergne and Alekseev-Torossian, MSRI, August 2008.
 Aarhus-0706: Algebraic Knot Theory, Århus University, June 2007.
Aarhus-0706: Algebraic Knot Theory, Århus University, June 2007.
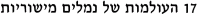 ,
The Hebrew University, January 2001.
,
The Hebrew University, January 2001.
 MSRI-001206: Finite type invariants and a strange breed of planar
algebras, MSRI December 2000.
MSRI-001206: Finite type invariants and a strange breed of planar
algebras, MSRI December 2000.
 CUNY-001205: On Links, Functions, Integrals and 3-Manifold Invariants, Einstein Chair Mathematics Seminar, CUNY, December 2000.
CUNY-001205: On Links, Functions, Integrals and 3-Manifold Invariants, Einstein Chair Mathematics Seminar, CUNY, December 2000.