
$\newcommand{\R}{\mathbb R }$ $\newcommand{\N}{\mathbb N }$ $\newcommand{\Z}{\mathbb Z }$ $\newcommand{\bfa}{\mathbf a}$ $\newcommand{\bfb}{\mathbf b}$ $\newcommand{\bff}{\mathbf f}$ $\newcommand{\bfu}{\mathbf u}$ $\newcommand{\bfx}{\mathbf x}$ $\newcommand{\bfy}{\mathbf y}$ $\newcommand{\ep}{\varepsilon}$
path-connected
The familiar Intermediate Value Theorem (abbreviated IVT) in 1d applies to a continuous function $f$ whose domain is an interval.
To state an analogue of the IVT in higher dimensions, we need to figure out what kind of domains the theorem should apply to.
A condition that is easy to state, intuitively reasonable, and good enough for all our purposes
is path-connectedness
. Informally, a set $S\subset \R^n$ is path-connected if
any two points in $S$ can be connected by a path that stays in $S$. More precisely:
Definition. A set $S\subset \R^n$ is path-connected if, for every pair of points $\bfx$ and $\bfy$ in $S$, \begin{equation}\label{pc1} \exists \mbox{ continuous }\ \gamma:[0,1]\to S, \mbox{ such that }\gamma(0) = \bfx, \qquad \gamma(1) = \bfy. \end{equation}
(As is usual with mathematics, different sources sometimes use different terms. For example, Folland uses the terms arcwise connected
or pathwise connected
in place of path-connected
.)
We emphasize that a key point in the definition is that $\gamma(s)$ is required to belong to $S$ for all $s\in [0,1]$
In general, our position will be that we can recognize path-connectedness when we see it. For example, consider the pictures below:

The set above is clearly path-connected set, and the set below clearly is not.
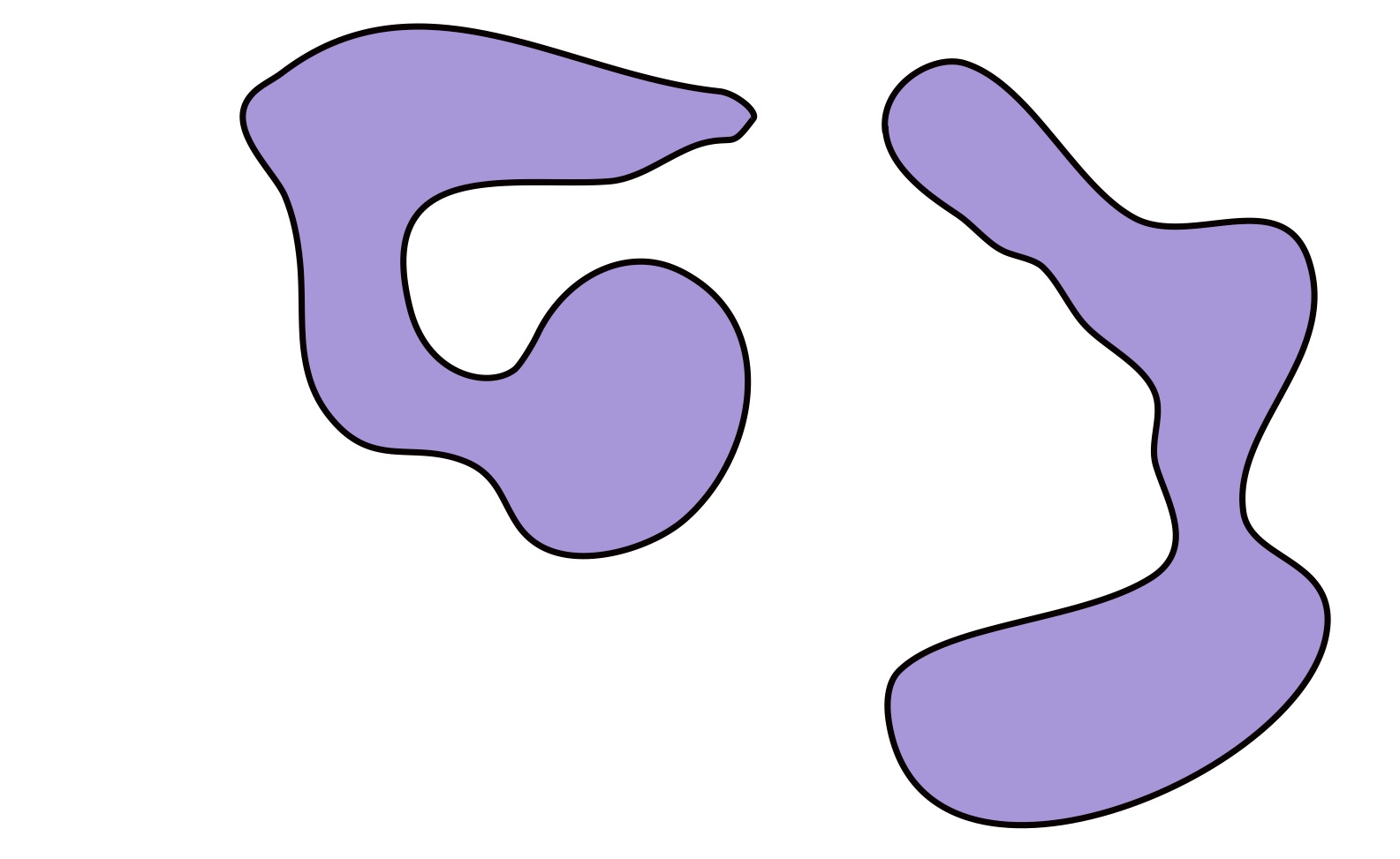
Because we can easily determine whether a set is path-connected by looking at it, we will not often go to the trouble of giving a rigorous mathematical proof of path-conectedness. If for some reason we decide to prove it, then normally the main point of a proof will be to write down in mathematical language an argument that captures our geometric intuition.
Here are a couple of examples:
Example 1. A ball $B(r,\bfa)$ is path-connected.
Our geometric intuition: This is clear, because if $\bfx, \bfy$ both belong to $B(r,\bfa)$, then from drawing a picture, we are confident that the straight line segment that starts at $\bfx$ and ends at $\bfy$ is a continuous path joining $\bfx$ to $\bfy$.
If we decide to prove it: then we can just write down the above
idea using mathematical language. We can interpret straight line segment that starts at $\bfx$ and ends at $\bfy$
as the function of the form
$$
\gamma(t) = \bfb +t {\bf m} \quad\mbox{ for vectors }\bfb, {\bf m}\in \R^n,
$$
where we will choose $\bfb$ and $\bf m$ so that $\gamma$ satisfies
$\gamma(0)=\bfx, \gamma(1) = \bfy$, as required.
This leads to
\begin{equation}\label{segment}
\boxed{ \gamma(t) = \bfx + t(\bfy - \bfx) = (1-t) \bfx + t\bfy }
\end{equation}
We have to check 3 things:
Remark. The formula \eqref{segment} for a path corresponding to a straight-line segment that starts at $\bfx$ and ends at $\bfy$ appears very frequently in mathematics, and should be committed to memory.
Example 2. If $S_1$ and $S_2$ are path-connected, and $S_1\cap S_2 \ne \emptyset$, then $S := S_1\cup S_2$ is path-connected.
Our geometric intuition: Consider any $\bfx$ and $\bfy$ in $S$.

To find a path connecting these two points, let $\bf z$ be an element of $S_1\cap S_2$.

Then since $\bf z$ and $\bfx$ both belong to either $S_1$ or $S_2$, we can find a continuous path connecting $\bfx$ to $\bf z$ that stays in that set, and hence in $S$.

Similarly we can find a continuous path connecting $\bf z$ to $\bfy$ that stays in $S$.

Now we can move continuously from $\bfx$ to $\bfy$, while staying inside $S$, by concatenating the paths, i.e. first following the continuous path from $\bfx$ to $\bf z$; then following the continuous path from $\bf z$ to $\bfy$.

In this way, we can find a path conecting any two points $\bfx$ and $\bfy$.
If we decide to prove it: we will just follow the above geometric intuition.
Suppose we are given any two points $\bfx, \bfy$ in $S_1\cup S_2$.
Fix a point ${\bf z}\in S_1\cap S_2$. Here we are using the hypothesis that $S_1\cap S_2\ne \emptyset$.
Since $\bfx$ belongs to either $S_1$ or $S_2$, and $\bf z$ belongs to both $S_1$ and $S_2$, it is clear that one of these two path-connected sets --- either $S_1$ or $S_2$ --- must contain both $\bfx$ and $\bf z$. Thus these two points can be connected by a path, say $\gamma_x$, that stays in this set, and hence inside $S = S_1\cup S_2$. That is, $$ \exists \mbox{ continuous }\gamma_x:[0,1]\to S \mbox{ such that }\gamma_x(0) = \bfx, \qquad \gamma_x(1) ={\bf z}. $$
By exactly the same reasoning, $$ \exists\mbox{ continuous }\gamma_y:[0,1]\to S \mbox{ such that }\gamma_y(0) = {\bf z}, \qquad \gamma_y(1) ={\bf y}. $$
Now we have to figure out how to write down our idea of joining the two paths together to obtain a single continuous function $\gamma:[0,1]\to S$ that starts that $\bfx$ and ends at $\bfy$. As a preliminary step, define $\widetilde \gamma:[0,2]\to S$ by \begin{equation}\label{tg} \widetilde \gamma(t) := \begin{cases} \gamma_x(t) &\mbox{ if }t\in [0,1]\\ \gamma_y(t-1) &\mbox{ if }t\in [1,2] \ . \end{cases} \end{equation} This satisfies $$ \widetilde \gamma\mbox{ is continuous}, \qquad \widetilde \gamma(0) = \bfx, \qquad \widetilde \gamma(2) = \bfy. $$ (The detailed $\ep-\delta$ proof of continuity is left as a practice problem for those who are interested.) The only problem is that we want a function that ends up at $\bfy$ at $t=1$ rather than $t=2$. But this is easy to fix, by defining $$ \gamma(t) := \widetilde \gamma(2t),\qquad t\in [0,1]. $$ Then $\gamma$ satisfies \eqref{pc1}. Since $\bfx$ and $\bfy$ were arbitrary points in $S = S_1\cup S_2$, it follows that $S$ is path-connected. $\quad \Box$
Having given the definition of path-connected and seen some examples, we now state an $n$-dimensional version of the Intermediate Value Theorem, for which path-connectedness is the main geometric hypothesis.
Theorem 1: the Intermediate Value Theorem. Assume that $S$ is a path-connected subset of $\R^n$ and that $f:S\to \R$ is continuous. If $\bfa, \bfb$ are points in $S$ and $$ \mbox{ either } f(\bfa) < t <f(\bfb), \qquad \mbox{ or }\quad f(\bfb) < t <f(\bfa), $$ then there exists a point ${\bf c} \in S$ such that $f({\bf c})=t$.
Proof.
Because $S$ is path-connected, there exists a continuous $\gamma:[0,1]\to S$ such that $\gamma(0)=\bfa$ and $\gamma(1) = \bfb$.
Now define $\phi: [0,1]\to \R$ by $\phi = f\circ \gamma$.
Because both $f$ and $\gamma$ are continuous, we know that $\phi$ is continuous. Also, by hypothesis $$ \mbox{ either } \ \ \phi(0) = f(\bfa) < t <f(\bfb)= \phi(1) , \qquad \mbox{ or }\quad \phi(1) = f(\bfb) < t <f(\bfa) =\phi(0). $$ So the Intermediate Value Theorem for functions of a single variable implies that there exists $s\in [0,1]$ such that $\phi(s) = t$.
But since $\phi(s) = f(\gamma(s))$, if we define ${\bf c} := \gamma(s)$, then ${\bf c} \in S$ and $f({\bf c})=t$. This proves the existence of a point $\bf c$ with the desired properties. $\quad\Box$
As with functions of a single variable, the theorem can be used to show that certain equations have solutions. The following example is a little artificial but it illustrates this point.
Example 3. Prove that the equation
$$
x^2+2y^2 = e^{(z-\frac 12)^2 cos(e^{-\sin (y/(x+2))}) }
$$
has a solution in the ball $B(2, {\bf 0})\subset \R^3$.
To solve this, let's rewrite the problem as $f(x,y,z)=0$ for $f(x,y,z) = x^2+2y^2 - e^{(z-\frac 12)^2 cos(e^{-\sin (y/(x+2))})}$. Note that $f(0,0,\frac 12) = -e^0 = -1<0$, and $f(0,1, 1/2) = 2-e^0 = 1>0$. Both of these points belong to $B(2,{\bf 0})$. We also know that balls are pathwise connected, so it follows from the Intermediate Value Theorem that there must exist some point in $B(2, {\bf 0})$ where $f=0$.
Example 4 Assume that $S$ is a subset of $\R^n$. The Intermediate Value Theorem implies if there exists a continuous function $f:S\to \R$ and a number $c\in \R$ and points $\bfa,\bfb\in S$ such that $$ f(\bfa)< c, \qquad f(\bfb)>c, \qquad f(\bfx)\ne c \mbox{ for any }\bfx\in S $$ then $S$ is not path-connected.
This can be used to prove that some sets $S$ are not path connected. For example, let $$ S := \{(x,y)\in \R^2 : x^2 - y^2 \ge 1 \}. $$ Let $f(x,y) = x$, and let $\bfa = (-1,0)$ and $\bfb= (1,0)$. Clearly $f(\bfa) = -1$ and $f(\bfb)=1$. But $S$ cannot contain any points where $f=0$, since $$ f(x,y)=0 \Rightarrow x=0 \Rightarrow x^2-y^2 = -y^2 \le 0 \Rightarrow (x,y)\not \in S. $$
Given an example of a set that is/is not path-connected
Determine (without proof) whether a given set is path-connected. For example, let $Q_j\subset \R^2$ denote the (open) $j$th quadrant, for $j=1,\ldots, 4$, so that $$ Q_1= \{(x,y)\in \R^2 : x>0\mbox{ and }y>0\}, \qquad Q_3= \{(x,y)\in \R^2 : x< 0\mbox{ and }y< 0\}, $$ Determine which of the following sets are path-connected:
Show that the equation $f(\bfx)= 0$ has a solution on the set $S = \cdots$. See Example 3 above. Strictly speaking, we should only ask this question when $S$ is a set that we have proved is path-connected, such as a ball.
Prove that the function $\widetilde \gamma$, defined in \eqref{tg}, is continuous.
Detrmine whether a set is path-connected, and explain why your answer is correct. Consider for example the same sets appearing in the Basic Skills
above.
(Recall that in this class, explain means: give a mathematical argument that may fall short of a full proof but that commnunicates a basic relevant mathematical idea. In this case, to explain why a set is path-connected, you might for example describe, in words, how to connect any two points in a set by a continuous path, without writing down a formula for the path.)
If $S_1$ and $S_2$ are path-connected sets in $\R^2$, must it be true that $S_1\cap S_2$ is path-connected? Explain your answer.
A set $S\subset \R^n$ is defined to be star-shaped about the origin if, $$ \mbox{ for every $\bfx \in S$ and every $\lambda\in [0,1]$ }, \qquad\mbox{ the point }\lambda \bfx \mbox{ belongs to $S$}. $$
Let
$$
S^+ := \{ \bfx = (x_1,\ldots, x_n)\in \R^n : |\bfx|=1, \ x_n \ge 0 \}.
$$
and
$$
S^- := \{ \bfx = (x_1,\ldots, x_n)\in \R^n : |\bfx|=1, \ x_n \le 0 \}.
$$
One might call these sets the upper (unit) hemisphere
and lower (unit) hemisphere
respectively.
Let $S$ denote the unit sphere in $\R^n$: $$ S := \{ \bfx \in \R^n : |\bfx|=1, \}. $$
Let $S$ denote the unit sphere in $\R^n$, as in the previous problem, and assume that
$f:S\to \R$ is continuous.
Prove that there exists some $\bfx\in S$ such that $f(\bfx) = f(-\bfx)$.
(This implies, for example, that at any given moment, there are two exactly antipodal points on the earth where the temperature is exactly the same.)
hints: