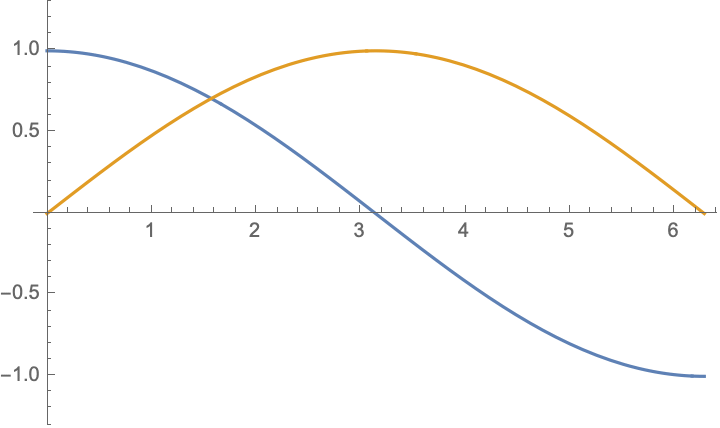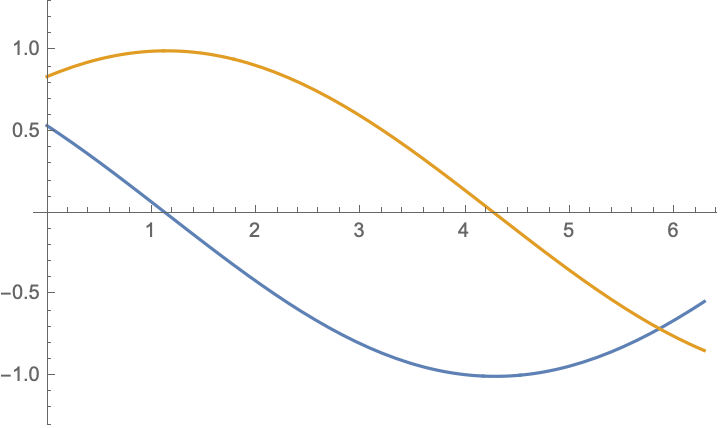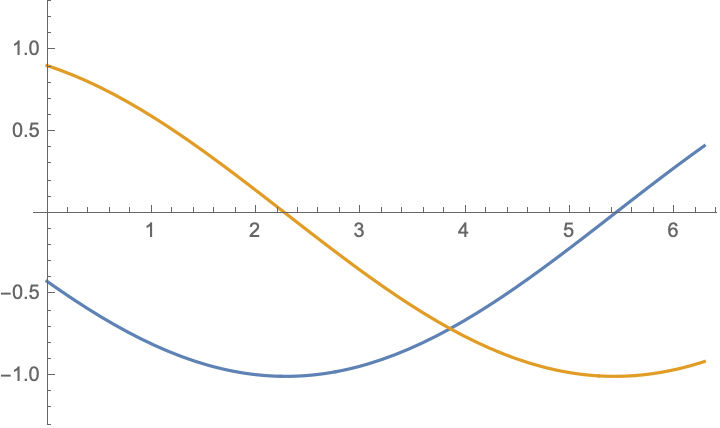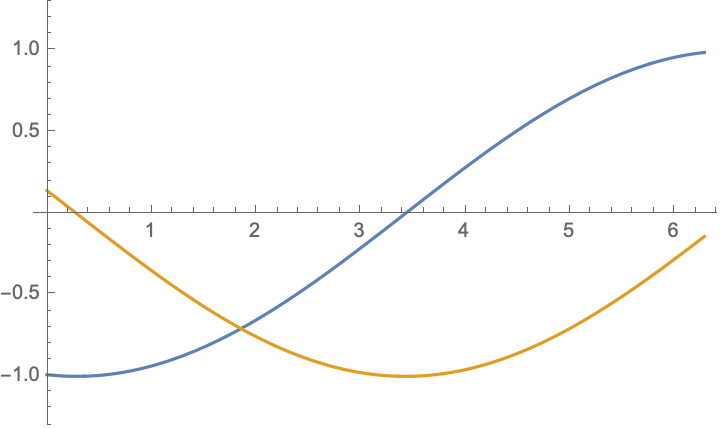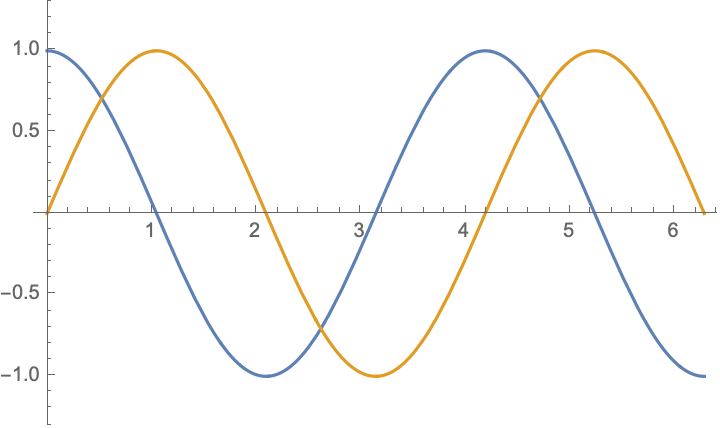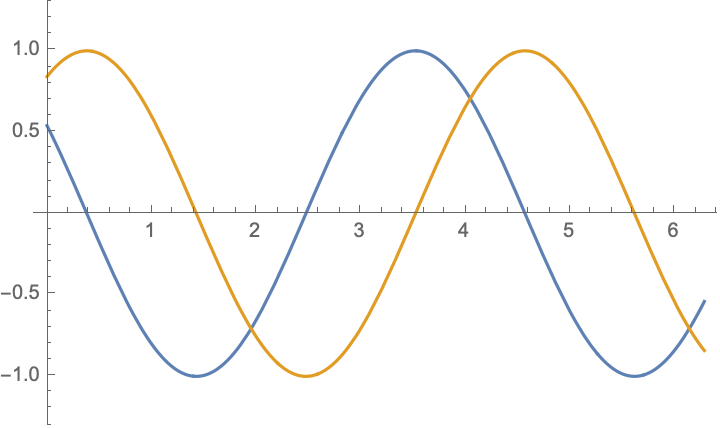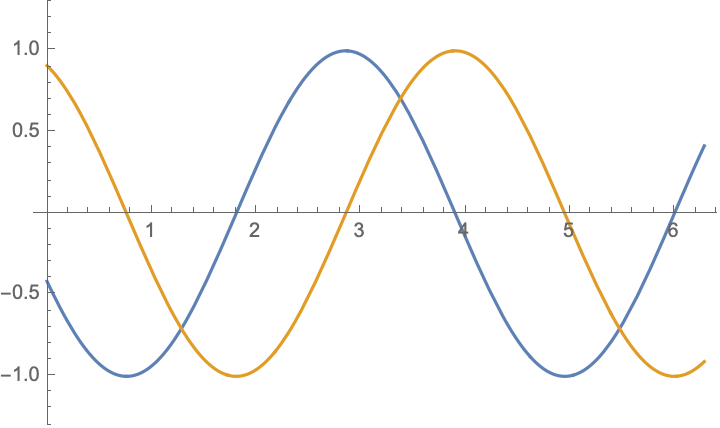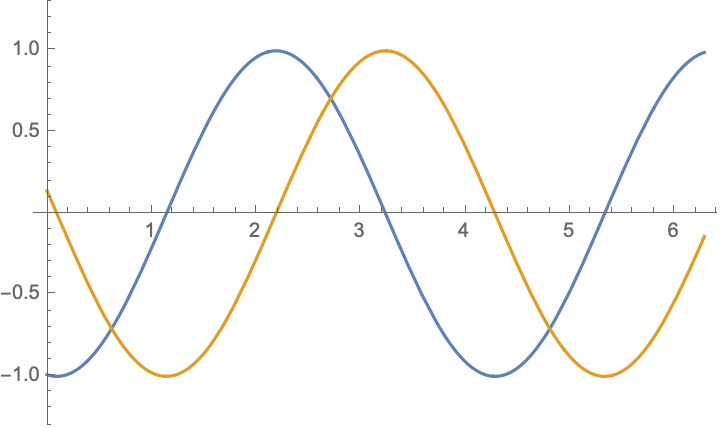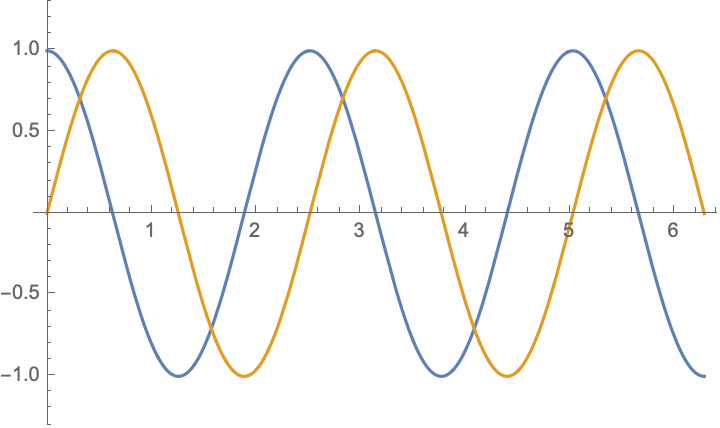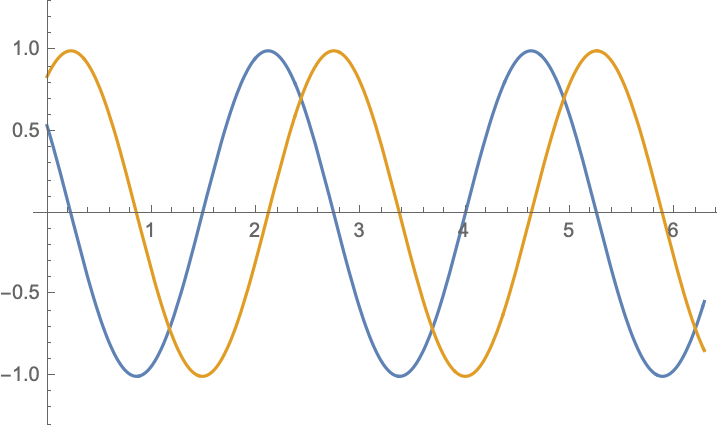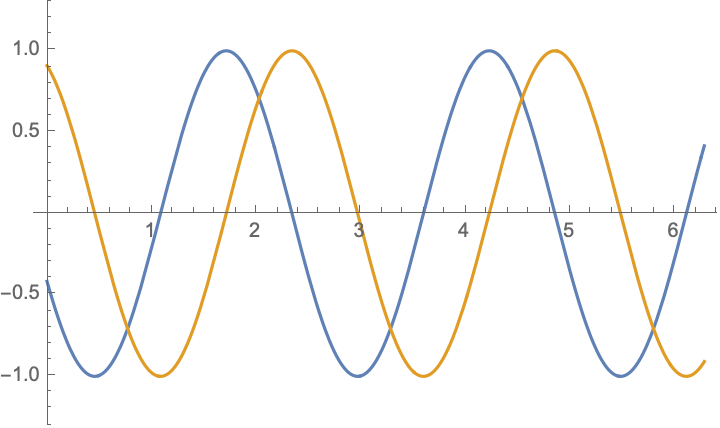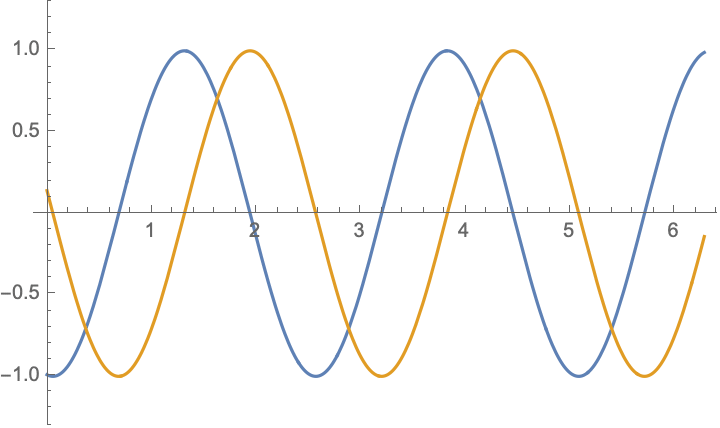$\renewcommand{\Re}{\operatorname{Re}}$ $\renewcommand{\Im}{\operatorname{Im}}$ $\newcommand{\erf}{\operatorname{erf}}$ $\newcommand{\dag}{\dagger}$ $\newcommand{\const}{\mathrm{const}}$ $\newcommand{\arcsinh}{\operatorname{arcsinh}}$

Fourier Method for $1$D Wave equation-Visualization

Antiperiodic

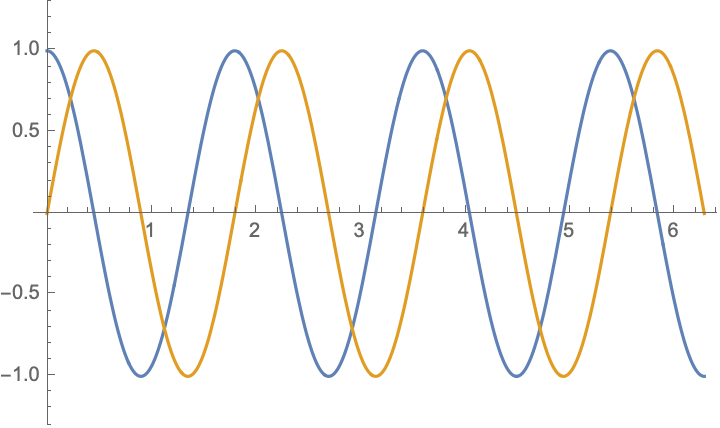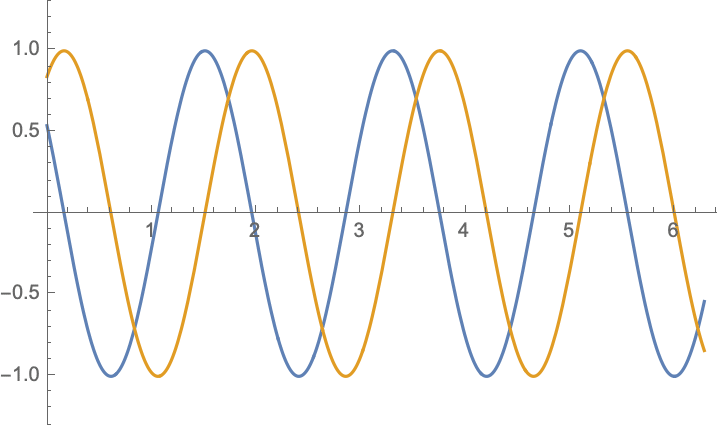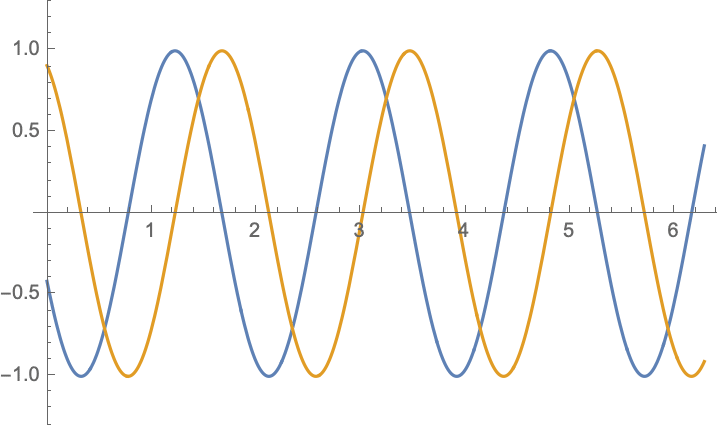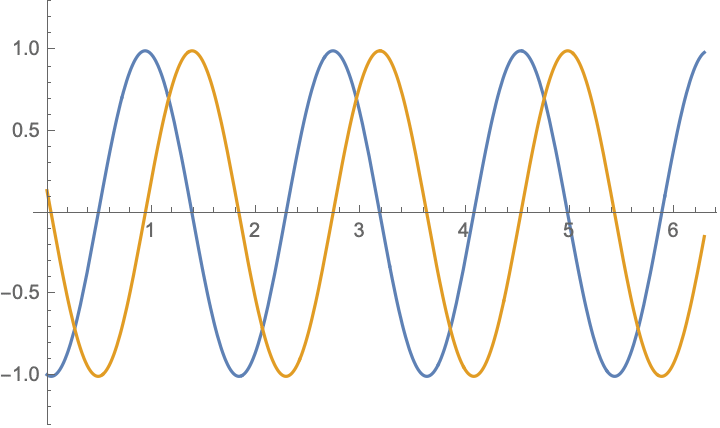
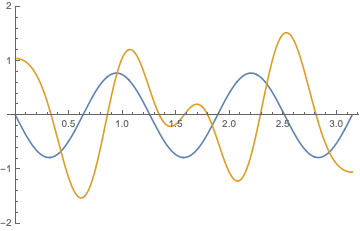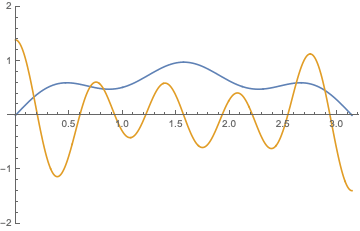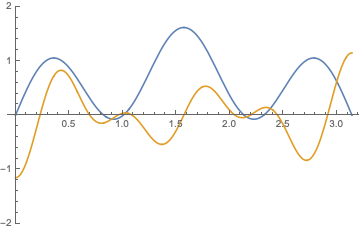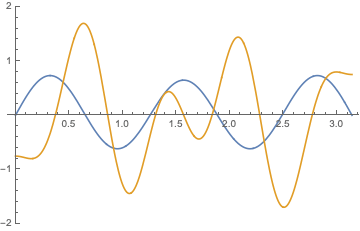
For boundary value problem $$\begin{aligned} &u_{tt}-c^2u_{xx}=0,\\ &u|_{x=0}=-u|_{x=l},&&u_x|_{x=0}=-u_x|_{x=l} \end{aligned}$$ there are simple solutions in the form $$ u(x,t)= \cos(\frac{n\pi ct}{2l})\cos(\frac{n\pi x}{2l})$$ and $$ u(x,t)= \cos(\frac{(2n-1)\pi ct}{l})\sin(\frac{(2n-1)\pi x}{l})$$ and their combinations $$u(x,t)= \exp[\frac{(2n-1)\pi i}{l}( x\pm ct)],\qquad n=\ldots,-2,-1,0,1,2,\ldots;$$ below are shown $\Re (u)$ and $\Im (u)$:

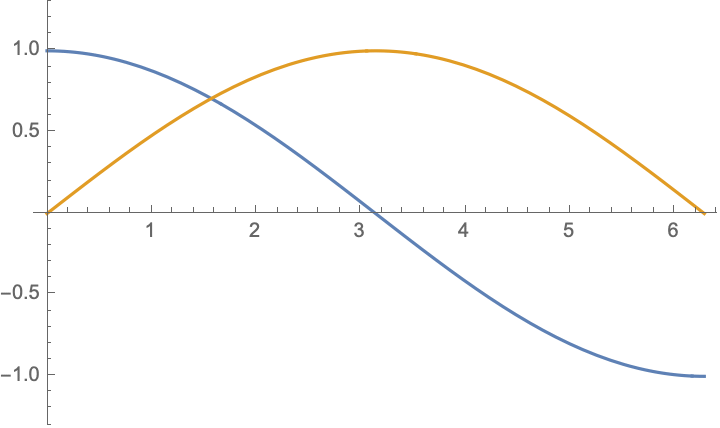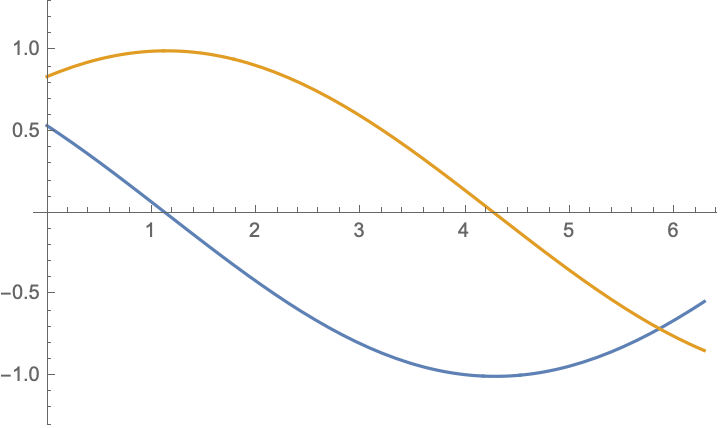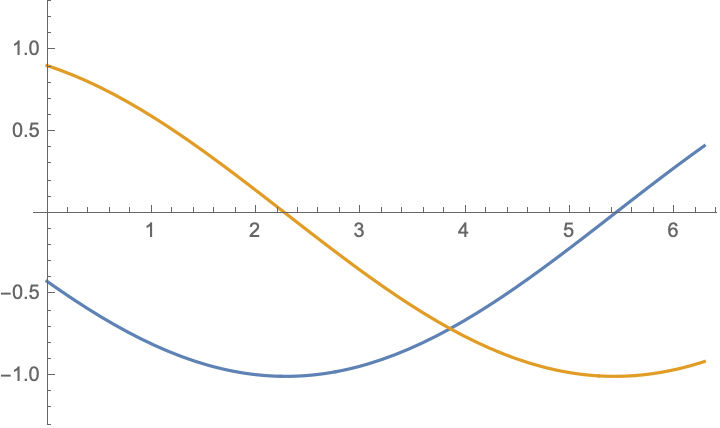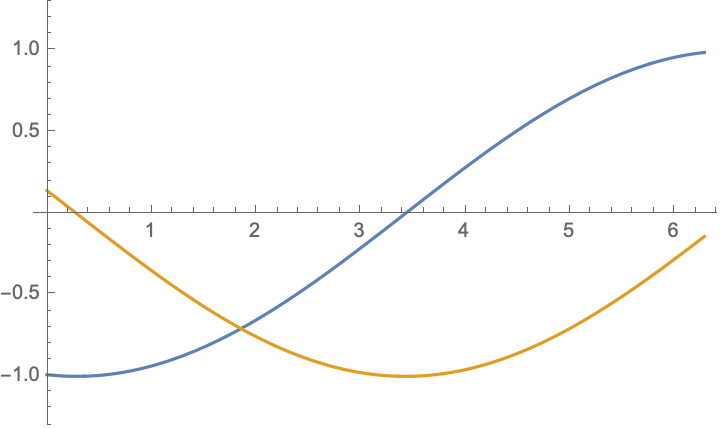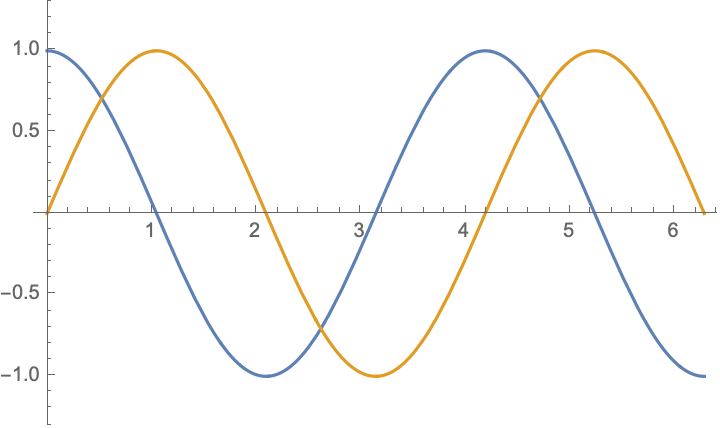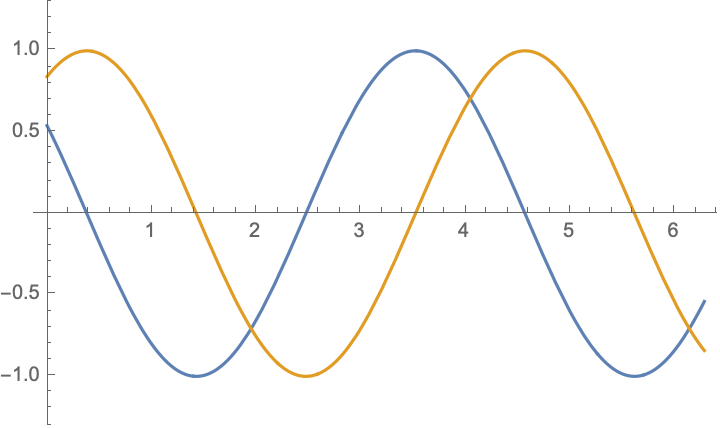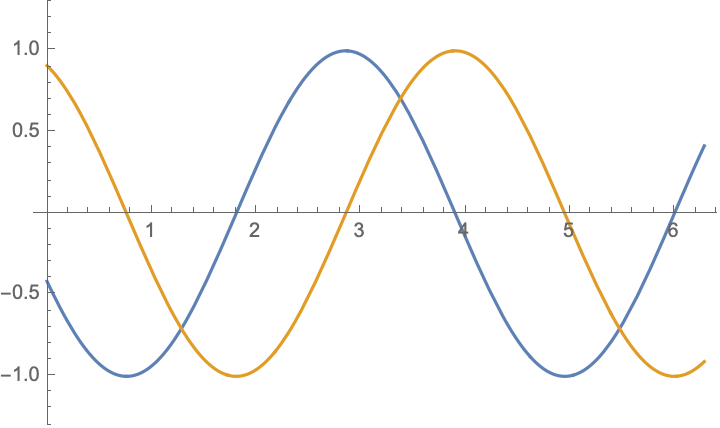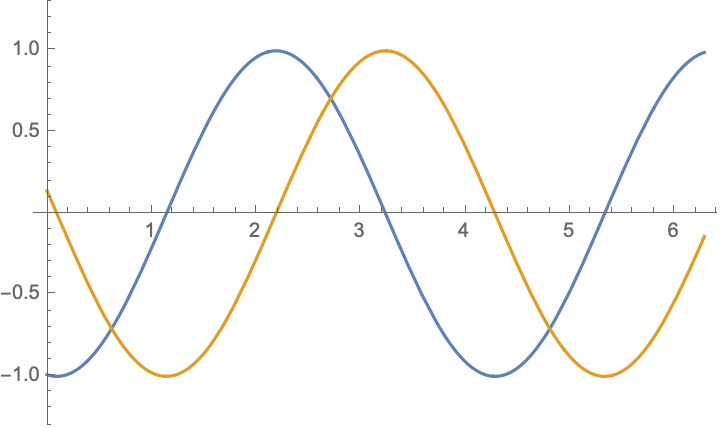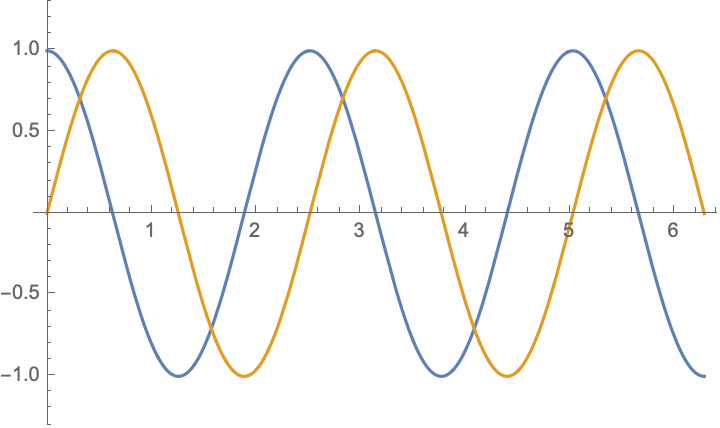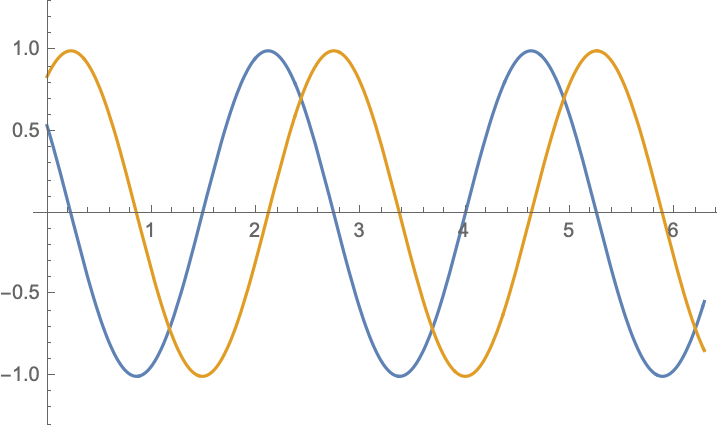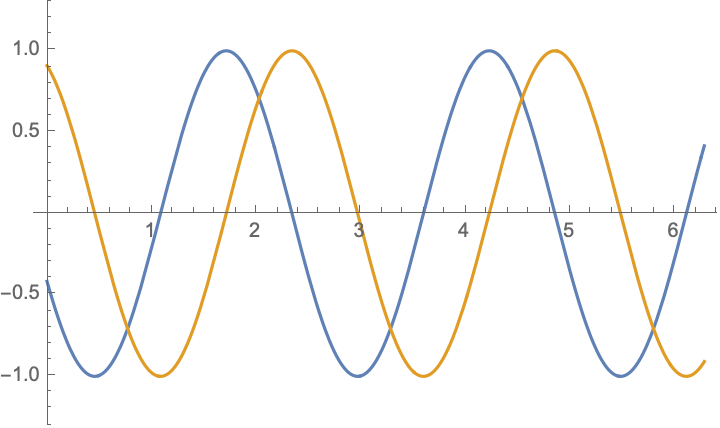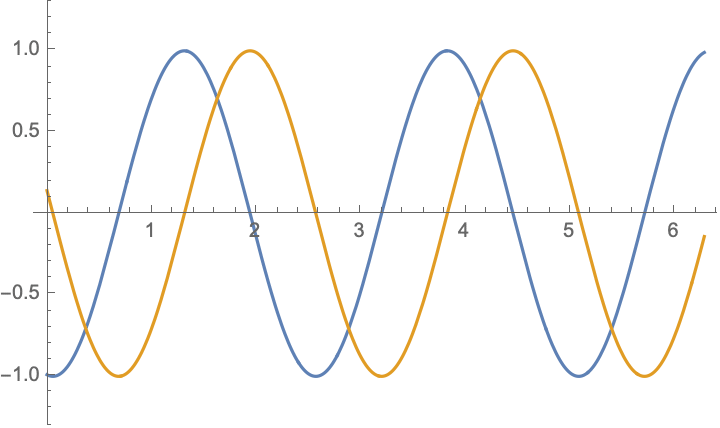and general solutions of in the form \begin{align*} u(x,t)= \sum_{n=1}^{\infty}&\Bigl[\bigl[A_n\cos(\frac{(2n-1)\pi ct}{l})+B_n\sin (\frac{(2n-1)\pi ct}{l})\bigr]\cos(\frac{(2n-1)\pi x}{l})+\\ &[\bigl[C_n\cos(\frac{(2n-1)\pi ct}{l})+D_n\sin (\frac{(2n-1)\pi ct}{l})\bigr]\sin(\frac{(2n-1)\pi x}{l})\Bigr] \end{align*} and their combinations $$ u(x,t)= \sum_{n=-\infty}^\infty \bigl[A_n \exp[\frac{(2n-1))\pi nct i}{l}]+ B_n \exp[-\frac{(2n-1)\pi nct i}{l}]\bigr]\exp( \frac{(2n-1) )\pi x i}{l});$$ below are shown $\Re (u)$ and $\Im (u)$:

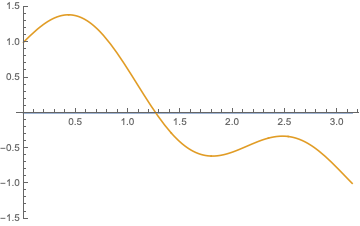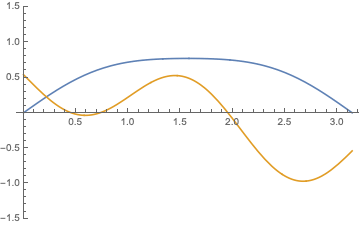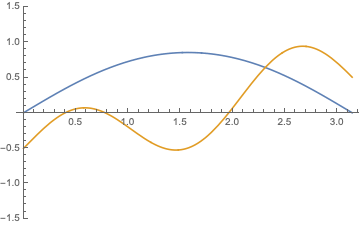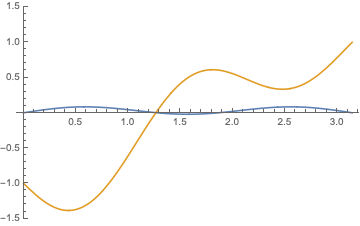(To restart animation just reload this page).