$\newcommand{\const}{\mathrm{const}}$
We realize that lines $x+ct=\const$ and $x-ct=\const$ play a very special role in our analysis. We call these lines characteristics. Let us introduce characteristic coordinates \begin{equation} \left\{\begin{aligned} &\xi=x+ct,\\ &\eta=x-ct. \end{aligned}\right. \label{eq-1} \end{equation} Proposition 4.1. \begin{equation} u_{tt}-c^2u_{xx}=-4c^2u_{\xi \eta}. \label{eq-2} \end{equation} Proof. From (\ref{eq-1}) we see that $x=\frac{1}{2}(\xi+\eta)$ and $t=\frac{1}{2c}(\xi-\eta)$ and therefore due to chain rule $v_\xi = \frac{1}{2}v_x+\frac{1}{2c}v_t$ and $v_\eta = \frac{1}{2}v_x-\frac{1}{2c}v_t$ and therefore \begin{equation*} -4c^2u_{\xi\eta}= -\frac{1}{4}(c\partial_x+\partial_t)(c\partial_x-\partial_t)u=u_{tt}-c^2u_{xx}.\tag*{QED} \end{equation*}
Therefore wave equation (3.1) [(3.1) means (1) from Lecture 3)] becomes in the characteristic coordinates \begin{equation} u_{\xi\eta}=0 \label{eq-3} \end{equation} which we rewrite as $(u_\xi)_\eta=0\implies u_\xi =\phi'(\xi)$ (really, $u_\xi$ should not depend on $\eta$ and it is convenient to denote by $\phi(\xi)$ the primitive of $u_\xi$). Then $(u-\phi(\xi))_\xi =0\implies u-\phi(\xi)=\psi(\eta)$ (due to the same arguments) and therefore \begin{equation} u=\phi(\xi)+\psi(\eta) \label{eq-4} \end{equation} is the general solution to (\ref{eq-3}).
Example. Consider Goursat problem for (\ref{eq-3}): \begin{gather*} u_{\xi\eta}=0\qquad \text{as } \xi>0,\eta>0\\[3pt] u|_{\eta=0}=g(\xi)\qquad \text{as } \xi>0 ,\\[3pt] u|_{\xi=0}=h(\eta)\qquad \text{as } \eta>0 \end{gather*} where $g$ and $h$ must satisfy compatibility condition $g(0)=h(0)$ (really $g(0)=u(0,0)=h(0)$).
Then one can see easily that $u(\xi,\eta)=g(\xi)+h(\eta)-g(0)$ solves Goursat problem.
Plugging (\ref{eq-1}) into (\ref{eq-4}) we get for a general solution (3.1) \begin{equation} u=\phi (x+ct)+\psi(x-ct) \label{eq-5} \end{equation} which is exactly (3.7).
So far we achieved nothing new. Consider now IVP:
\begin{align}
&u_{tt}-c^2u_{xx}=f(x,t),\label{eq-6} \\[3pt]
&u|_{t=0}=g(x),\label{eq-7}\\[3pt]
&u_t|_{t=0}=h(x). \label{eq-8}
\end{align}
It is convenient for us to assume that $g=h=0$. Later we will get rid off this assumption.
Rewriting (\ref{eq-6}) as
\begin{equation*}
\tilde{u}_{\xi\eta}= -\frac{1}{4c^2}\tilde{f}(\xi,\eta )
\end{equation*}
[where $\tilde{u}$ etc means that we use characteristic coordinates] we get after integration
\begin{equation*}
\tilde{u}_{\xi}= -\frac{1}{4c^2}\int^\eta \tilde{f}(\xi,\eta' )\,d\eta'=
-\frac{1}{4c^2}\int_\xi ^\eta \tilde{f}(\xi,\eta' )\,d\eta'{\color{red}{+ \phi'(\xi)}}
\end{equation*}
with an indefinite integral in the middle. Note that $t=0$ means exactly that $\xi=\eta$ but then $u_\xi=0$ there. Really, $u_\xi$ is a linear combination of $u_t$ and $u_x$ but both of them are $0$ as $t=0$. Therefore $\phi'(\xi)=0$ and
\begin{equation*}
\tilde{u}_{\xi}= \frac{1}{4c^2}\int^\xi _\eta \tilde{f}(\xi,\eta' )\,d\eta'
\end{equation*}
where we flipped limits and changed sign.
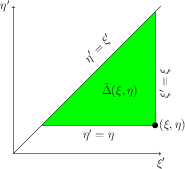
Integrating with respect to $\xi$ we arrive to \begin{equation*} \tilde{u}= \frac{1}{4c^2} \int^\xi \Bigl[\int_{\xi'} ^\eta \tilde{f}(\xi',\eta' )\,d\eta'\Bigr]\,d\xi' = \int_\eta ^\xi \Bigl[\int_\eta ^{\xi'} \tilde{f}(\xi',\eta' )\,d\eta'\Bigr]\,d\xi' {\color{red}{+ \psi(\eta)}} \end{equation*} and $\psi(\eta)$ also must vanish because $u=0$ as $t=0$ (i.e. $\xi=\eta$). So \begin{equation} \tilde{u}(\xi,\eta)= \frac{1}{4c^2} \int_\eta ^\xi \Bigl[\int_\eta ^{\xi'} \tilde{f}(\xi',\eta' )\,d\eta'\Bigr]\,d\xi' . \label{eq-9} \end{equation} We got a solution as a double integral but we want to write it down as 2-dimensional integral \begin{equation} \tilde{u}(\xi,\eta)= \frac{1}{4c^2} \iint_{\tilde{\Delta}(\xi,\eta)} \tilde{f}(\xi',\eta' )\,d\eta’d\xi' . \label{eq-10} \end{equation} But what is $\tilde{\Delta}$? Consider $\xi>\eta$. Then $\xi'$ should run from $\eta$ to $\xi$ and for fixed $\xi'$, $\eta<\xi'<\xi$ eta should run from $\eta $ to $\xi'$. So, we get a triangle bounded by $\xi'=\eta'$, $\xi'=\xi$ and $\eta'=\eta$:

But in coordinates $(x,t)$ this domain $\Delta(x,t)$ is bounded by $t=0$ and two characteristics:
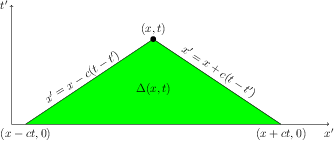
So, we get \begin{equation} u(x,t)= \frac{1}{2c} \iint_{\Delta (x,t)} f(x',t' )\,dx’d t' . \label{eq-11} \end{equation} because we need to replace $d\xi’d\eta' $ by $|J|dx'dt'$ with Jacobian $J$.
Exercise. Calculate $J$ and justify factor $2c$.