$\renewcommand{\Re}{\operatorname{Re}}$ $\newcommand{\erf}{\operatorname{erf}}$ $\newcommand{\dag}{\dagger}$ $\newcommand{\const}{\mathrm{const}}$
Consider wave equation \begin{equation} u_{tt}-c^2\Delta u=0. \label{equ-29.1} \end{equation} Multiplying by $u_t$ we arrive to \begin{multline*} 0=u_t u_{tt}-c^2 u_t\Delta u= \frac{1}{2}\partial_t (u_{t}^2)-c^2\nabla \cdot (u_t\nabla u) + c^2\nabla u_t \cdot \nabla u =\\ \frac{1}{2}\partial_t \bigl(u_{t}^2+c^2|\nabla u|^2\bigr)- c^2\nabla \cdot (u_t\nabla u) \end{multline*} that is \begin{equation} \frac{1}{2}\partial_t \bigl(u_{t}^2+c^2|\nabla u|^2\bigr)- c^2\nabla \cdot (u_t\nabla u)=0. \label{equ-29.2} \end{equation} This is an energy conservation law in the local form.
If we integrate over domain $\Omega\subset \mathbb{R}_t\times \mathbb{R}_x^n$ we arrive to \begin{equation} \iint_{\Sigma} \Bigl( \bigl(u_{t}^2+|\nabla u|^2\bigr)\nu_t -c^2 u_t \nabla u \cdot \nu_x\Bigr) \,d\sigma=0 \label{equ-29.3} \end{equation} where $\Sigma$ is a boundary of $\Omega$, $\nu$ is an external normal and $d\sigma$ is an alement of "area"; $\nu_t$ and $\nu_x$ are its $t$ and $x$ components.
Consider a quadratic form \begin{equation} Q(U_0,\mathbf{U})=U_0^2 +|\mathbf{U}|^2 - 2U_0 c\nu_t^{-1}\nu_x\cdot \mathbf{U}. \label{equ-29.4} \end{equation}
If $c|\nu_x|<|\nu_t|$ then $Q$ is positive definite (i.e. $Q(U_0,\mathbf{U})\ge 0$ and $Q(U_0,\mathbf{U})=0$ iff $U_0=\mathbf{U}=0$);
If $c|\nu_x|=|\nu_t|$ then $Q$ is non-negative definite (i.e. $Q(U_0,\mathbf{U})\ge 0$);
If $c|\nu_x|>|\nu_t|$ then $Q$ is not non-negative definite.
Proof is obvious.
If $c|\nu_x|<|\nu_t|$ then $\Sigma$ is space-like surface (in the given point).
If $c|\nu_x|=|\nu_t|$ then $\Sigma$ is *characteristic * (in the given point).
If $c|\nu_x|>|\nu_t|$ then $\Sigma$ is stime-like surface (in the given point).
Remark 1. Those who studied special relativity can explain (a), (c).
Consider now bounded domain $\Omega$ bounded by $\Sigma=\Sigma_+\cup\Sigma_-$ where $c|\nu_x|\le -\nu_t$ at each point of $\Sigma_-$ and $c|\nu_x|\le \nu_t$ at each point of $\Sigma_+$. Assume that $u$ satisfies (\ref{equ-29.1}) \begin{equation} u=u_t=0 \qquad \text{on }\ \Sigma_-. \label{equ-29.5} \end{equation} Then (\ref{equ-29.3}) implies that \begin{equation*} \iint_{\Sigma_+} \Bigl(\bigl(u_{t}^2+|\nabla u|^2\bigr)\nu_t - c^2 u_t \nabla u \cdot \nu_x\Bigr)\,d\sigma=0 \end{equation*} which due to assumption about $\Sigma_+$ implies that integrand is $0$ and therefore $u_t=\nabla u=0$ in each point where $c|\nu_x|<\nu_t$.

We can apply the same arguments to $\Omega_T:=\Omega \cap \{t<T\}$ with the boundary $\Sigma_T= \Sigma \cap \{t<T\}\cup S_T$, $S_T:=\Omega\cap\{t=T\}$; note that on $S_T$ $\nu_t=1$, $\nu_x=0$.
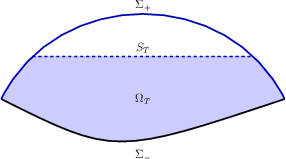
Therefore $u_t=\nabla u=0$ on $S_T$ and since we can select $T$ arbitrarily we conclude that this is true everywhere in $\Omega$. Since $u=0$ on $\Sigma_-$ we conclude that $u=0$ in $\Omega$. So we proved:
Theorem 1. Consider a bounded domain $\Omega$ bounded by $\Sigma=\Sigma_+\cup\Sigma_-$ where $c|\nu_x|\le -\nu_t$ at each point of $\Sigma_-$ and $c|\nu_x|\le \nu_t$ at each point of $\Sigma_+$. Assume that $u$ satisfies (\ref{equ-29.1}), (\ref{equ-29.5}). Then $u=0$ in $\Omega$.
It allows us to prove
Theorem 2. Consider $(y,\tau)$ with $\tau>0$ and let $K^-(y,\tau)= \{(x,t): t\le \tau, |y-x|<c(\tau-t)\}$ be a backward light cone issued from $(y,\tau)$. Let
Then $u=0$ in $K^-(x,t)\cap \{t>0\}$.
Proof is obvious: we can use $\Omega=K^-(x,t)\cap \{t>0\}$. Note that the border of $K^-(x,t)$ is characteristic at each point and $\nu_t>0$.
Consider domain $\mathcal{D}\subset \mathbb{R}^n$ with a boundary $\Gamma$.
Theorem 3. Consider $(y,\tau)$ with $\tau>0$ and let $K^-(y,\tau)= \{(x,t): t\le \tau, |y-x|<c(\tau-t)\}$ be a backward light cone issued from $(y,\tau)$. Let
Then $u=0$ in $K^-(y,\tau)\cap \{t>0\}\cap \{ x\in \mathcal{D}\}$.
Proof uses the same energy approach but now we have also integral over part of the surface $K^-(y,\tau)\cap \{t>0\}\cap \{ x\in \Gamma \}$ (which is time-like) but this integral is $0$ due to (c).
The energy approach works in a very general framework and is used not only to prove unicity but also an existence and stability of solutions.