$\renewcommand{\Re}{\operatorname{Re}}$ $\newcommand{\erf}{\operatorname{erf}}$ $\newcommand{\dag}{\dagger}$ $\newcommand{\const}{\mathrm{const}}$
Consider Gauss formula \begin{equation} \int_{\Omega} \nabla\cdot \mathbf{U}\,dV = - \int_\Sigma \mathbf{U}\cdot \nu\, dS \label{eq-1} \end{equation} where $\Omega$ is a bounded domain with the boundary $\Sigma$, $dV$ is a volume lement, $dS$ is an area element, $d\nu$ is a unit interior normal to $\Sigma$ , $\mathbf{U}$ is a vector field and $\nabla\cdot\mathbf{U}$ its divergence.
Remark. Usually $\nu$ would denote an exterior normal and then there would be no sign $-$ on the right of (\ref{eq-1}).
Let us plug $\mathbf{U}=\nabla u$ into (\ref{eq-1}). We get \begin{equation} \int_{\Omega} \Delta u\,dV = - \int_\Sigma \frac{\partial u}{\partial \nu}\, dS \label{eq-2} \end{equation} where $\Delta u=\nabla\cdot \nabla u$ is Laplacian of $u$, $\frac{\partial u}{\partial \nu}=\nabla u\cdot \nu$ is a derivative of $u$ in direction $\nu$.
Let us plug $\mathbf{U}=\nabla u$ into (\ref{eq-1}). We get \begin{equation} \int_{\Omega} \bigl(w\Delta u+\nabla u\cdot \nabla w\bigr)\,dV = - \int_\Sigma w\nabla u\cdot \nu\, dS. \label{eq-3} \end{equation} Antisymmetrizing (\ref{eq-3}) by $u,w$ (permutting $u$, $w$ and subtracting from original formula) we get \begin{equation} \int_{\Omega} \bigl(w\Delta u-u\Delta w\bigr)\,dV = \int_\Sigma \bigl(u\frac{\partial w}{\partial \nu}-w\frac{\partial u}{\partial \nu}\bigr)\, dS. \label{eq-4} \end{equation}
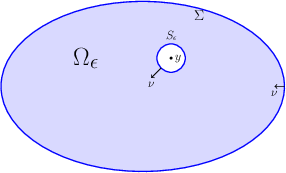
Consider now point $y$ not on $\Sigma$ and a function $w=|x-y|^{2-n}$ where $n$ is a dimension (as $n=2$ we take $w=-\log |x-y|$). As $y\in \Omega$ e cannot plug it in our formulae as $w$ is singular at $x=y$. So we consider $B_\epsilon$ ball of small radius $\epsilon$ with a center $y$ , $\Omega_\epsilon=\Omega \setminus B_\epsilon $ domain $\Omega$ with removed $B_\epsilon$ and $\Sigma_\epsilon=\Sigma \cup S_\epsilon$ its boundary, where $S_\epsilon$ is the sphere of radius $\epsilon$ with a center $y$. We get \begin{multline} \int_{\Omega_\epsilon} \bigl(w\Delta u-u\Delta w\bigr)\,dV = \int_\Sigma \bigl(u\frac{\partial w}{\partial \nu}-w\frac{\partial u}{\partial \nu}\bigr)\, dS+\\ \int_{S_\epsilon} \bigl(u\frac{\partial w}{\partial \nu}-w\frac{\partial u}{\partial \nu}\bigr)\,dS. \qquad \label{eq-5} \end{multline}

Let us consider the last term in (\ref{eq-5}) as $\epsilon \to 0$. Note that on $S_\epsilon$ $w=\epsilon^{2-n}$ and therefore $|\int_{S_\epsilon} w \frac{\partial u}{\partial \nu}\,dS|$ does not exceed $C\epsilon^{n-1}\times \epsilon^{2-n}=C\epsilon$ so it tends to $0$. We used that the area of $S_\epsilon$ is $\sigma_n \epsilon^{n-1}$ (where $\sigma_2=2\pi$, $\sigma_3=4\pi$, É)
For $\int_{S_\epsilon} u \frac{\partial w}{\partial \nu}\,dS$ we need more sophisticated arguments because $\frac{\partial w}{\partial \nu}= (n-2)\epsilon^{1-n}$ on $S_\epsilon$ (really, here $\nu$ is a radial direction away from $y$; as $n=2$ we get $-\epsilon^{-1}$). Consider \begin{equation} \int_{S_\epsilon} u \frac{\partial w}{\partial \nu}\,dS= \int_{S_\epsilon} \bigl(u-u(y)\bigr) \frac{\partial w}{\partial \nu}\,dS+ u(y) \int_{S_\epsilon} \frac{\partial w}{\partial \nu}\,dS \label{eq-6} \end{equation} (old trick to add and subtract constant). An absolute value of the first term does not exceed $C\max _{x\in S_\epsilon} |u(x)-u(y)|\to 0$ as $\epsilon\to 0$. The first term just equals $(n-2)\sigma_n u(y)$.
Note that $\Delta w=0$ as $x\ne y$ (Home Assignment 8, problem 1). Therefore (\ref{eq-5}) becomes \begin{equation*} \int_{\Omega} w\Delta u\,dV = \int_\Sigma \bigl(u\frac{\partial w}{\partial \nu}-w\frac{\partial u}{\partial \nu}\bigr)\, dS+ (n-2)\sigma_n u(y)\qquad \end{equation*} where the term on the left is a usual improper integral and we have proven
Theorem 1. As $\Omega$ is bounded domain with a boundary $\Sigma$, and $y\in \Omega $ (and in particular, $y\notin \Sigma$) \begin{multline} u(y)=\int_{\Omega} G(x,y)\Delta u(x)\,dV + \\ \int_\Sigma \bigl(-u(x)\frac{\partial G}{\partial \nu_x}(x,y)+G(x,y)\frac{\partial u}{\partial \nu}(x)\bigr)\, dS \quad \label{eq-7} \end{multline} with \begin{equation} G(x,y)=\left\{\begin{aligned} -&\frac{1}{(n-2)\sigma_n}|x-y|^{2-n}&& n\ne 2,\\ -&\frac{1}{4\pi}|x-y|^{-1} &&n=3,\\ &\frac{1}{2\pi}\log |x-y| &&n=2,\\ &\frac{1}{2} |x-y| &&n=1. \end{aligned}\right. \label{eq-8} \end{equation}
Definition 1. $G(x,y)$ is a potential. In particular, as $n=3$ we get a Coulomb potential (aka Newton potential), and as $n=2$ we get a logarithmic potential.
Therefore if we know that $\Delta u=f$ in $\Omega$, $u|_\Sigma =g$ and $\frac{\partial u}{\partial \nu}=h$ (which is overdetermined problem as only one boundary condition is in fact needed) we get \begin{align} u(y)=&\int_{\Omega} G(x,y)f(x)\,dV \label{eq-9}\\ +& \int_\Sigma G(x,y)h(x)\, dS \notag\\ -& \int_\Sigma g(x)\frac{\partial G}{\partial \nu_x}\, dS.\notag \end{align}
The first term in the right-hand expression is a potential created by a charge with density $f$,
The second term in the right-hand expression is a potential created by a charge with surface density $h$ (aka single layer potential),
The third term in the right-hand expression is a double layer potential.
In fact we can consider two surfaces $\Sigma_-=\Sigma$ and $\Sigma_+$ on the distance exactly $\varepsilon$ from $\Sigma$ on its "outer" side and density $-\varepsilon^{-1}g$ on $\Sigma_-$ and $\varepsilon g$ on $\Sigma+$ (we can extend $g$ and as long as this extension is smooth it does not matter how), consider corresponding single layer potential, and then tend $\varepsilon\to +0$.
It is known that volume on $n$-dimensional ball is \begin{equation*} \omega_n=\left\{\begin{aligned} & \frac{\pi^{n/2}} {(n/2)!}&&\text{for even }\ n,\\ & \frac{2^{(n+1)/2}\pi^{(n-1)/2}}{n!!}&&\text{for odd }\ n, \end{aligned}\right. \end{equation*} where $m!!=m(m-2)(m-4)\ldots$ (the last factor $2$ or $1$ for even and odd $m$) and $\sigma_n=n\omega_n$.
This formula (\ref{eq-9}) as we expand $\Omega$ to the whole space becomes $\mathbb{R}^n$
Theorem 2. Let $n\ge 3$. If $f$ decays fast enough at infinity then \begin{equation} u(y)=\int_{\mathbb{R}^n} G(x,y)\Delta u(x)\,dV \label{eq-10} \end{equation} solves equation \begin{equation} \Delta u=f \label{eq-11} \end{equation} with conditions at infinity \begin{align} & u=O(r^{2-n}),\label{eq-12}\\ & \partial_r u =O(r^{1-n})&&\text{as }\ r=|x|\to \infty\label{eq-13} \end{align}
Consider $\Omega$ a ball of radius $r$ with a center in $y$. Let $u$ be a harmonic function (i.e. $\Delta u=0$) in $\Omega$. Then
Breaking the second term of (\ref{eq-7}) into \begin{equation*} -\int_\Sigma u(x)\frac{\partial G}{\partial \nu_x}(x,y)\,dS +\int_\Sigma G(x,y)\frac{\partial u}{\partial \nu}(x)\, dS \end{equation*} in the second part we can drag factor $G(x,y)$ out of integral where remains $\int_\Sigma \frac{\partial u}{\partial \nu}\, dS=-\int_V \Delta u\,dV=0$
In the first part we can drag factor $\frac{\partial G}{\partial \nu_x}$ out of integral where remains $\int_\Sigma u\,dS$ and we get \begin{equation} u(y)= \frac{1}{\sigma_n r^{n-1}} \int_\Sigma u(x)\, dS. \label{eq-14} \end{equation} So we proved
If $u$ is harmonic in the ball $B(y,r)$ of radius $r$ then in its center $y$ the value of $u$ is a mean value of $u$ over the sphere $S(y,r)$ bounding this ball.
If $u$ is harmonic in the ball $B(y,r)$ of radius $r$ then in its center the value of $u$ is a mean value of $u$ over this ball.
To prove (b) one should note from (a) that $\int _{S(y,\rho)}u(x)\,dS= \sigma_n \rho^{n-1}u(y)$ for any $\rho\in (0,r)$ and then \begin{equation*} \int _{B(y,r)}u(x)\,dx= \int_0^r\bigl(\int _{S(y,\rho)}u(x)\,dS\bigr)\,dr= u(y) \times \sigma_n\int_0^r \rho^{n-1}\,d\rho \end{equation*} and that $\sigma_n\int_0^r \rho^{n-1}\,d\rho$ is a volume of $B(y,r)$.
If $u$ is a harmonic function in the bounded domain $\Omega$ with a boundary $\Sigma$ then
$\max_\Omega u=\max_\Sigma u$ and $\min_\Omega u=\min_\Sigma u$;
If $\Omega$ is connected and $u(y)=\max_\Omega u$ (or $u(y)=\min_\Omega u$) for some inner point $y$ then $u=\const$.
Proof. Assume that $u(y)=\max_\Omega u$ for some inner point $y$. Consider the largest ball $B(y,r)$ containing in $\Omega$. By mean-value theorem $u(y)$ is a mean-value of $u$ over this ball but it is also a maximal value of $u$ in this ball and therefore $u(x)=u(y)$ in this ball. Then any point on $S(y,r)$ could be used as a "new $y$" and we can continue. Eventually each point of $x$ which could be connected to $y$ by a continuous curve inside of $\Omega$ will be covered and then in this point $u(x)=u(y)$. So, in the connected component of $\Omega$ containing $y$ $u=u(y)$ and it will be true on its border. Then $\max_\Sigma u\ge u(y)= \max_\Omega u$; but $\max_\Omega u\ge \max_\Sigma u$ and therefore (a) has been proven.
It also proves (b) as now we assume that $\Omega$ is connected.
Let $\Omega$ be a bounded domain. Then solution of Dirichlet problem in $\Omega$ for Laplace equation is unique.
Let $\Omega$ be an unbounded domain. Then solution of Dirichlet problem in $\Omega$ for Laplace equation is unique under condition at infinity: $|u|\to 0$ as $|x|\to \infty$.
Proof.
Consider $u$ solving $\Delta u=0$, $u|_\Sigma=0$ )and satisfying condition at infinity in (b)).
Due to maximum and minimum principle \begin{equation*} 0=\min_\Sigma u \le u(y) \le \max_\Sigma u =0\qquad \text{for }\ y\in \Omega. \end{equation*}
Consider ball $B(0,R)$ and domain $\Omega_R=\Omega \cap B(0,R)$. Its boundary is $\Sigma_R:=(\Sigma \cap B(0,R))\cup (\Omega \cap S(0,R))$. Then as $R\ge |y|$ \begin{equation*} \min_{\Sigma_R} u \le u(y) \le \max_{\Sigma_R}u \end{equation*} but \begin{equation} \min_{\Sigma_R} u = \min \bigl(\min_{\Sigma \cap B(0,R)}u, \min_{\Omega \cap S(0,R)} u\bigr) \label{eq-15} \end{equation} if $\Sigma \cap B(0,R)\ne \emptyset$, otherwise the we get just $\min_{\Omega \cap S(0,R)} u$. However $\min_{\Omega \cap S(0,R)} u\to 0$ as $R\to \infty$ due to condition to infinity. Also $\min_{\Sigma \cap B(0,R)}u=0$ and therefore the left-hand expression in (\ref{eq-15}) tends to $0$ as $R\to \infty$.
Similarly the right-hand expression in (\ref{eq-15}) tends to $0$ as $R\to \infty$ and we have $0\le u(y)\le 0$.