$\newcommand{\erf}{\operatorname{erf}}$ $\newcommand{\const}{\mathrm{const}}$
Example 1 (Dirichlet-Dirichlet; from Lecture 12). Eignevalue problem \begin{align} & X'' +\lambda X=0 && 0<x<l,\\[3pt] & X(0)=X(l)=0 \end{align} has eigenvalues and corresponding eigenfunctions \begin{align} & \lambda_n=\bigl(\frac{\pi n}{l}\bigr)^2,&&n=1,2,\ldots\\[3pt] & X_n=\sin \bigl(\frac{\pi n}{l}x\bigr). \end{align}
Example 2 (Neumann-Neumann). Eignevalue problem \begin{align} & X'' +\lambda X=0 && 0<x<l,\\[3pt] & X'(0)=X'(l)=0 \end{align} has eigenvalues and corresponding eigenfunctions \begin{align} & \lambda_n=\bigl(\frac{\pi n}{l}\bigr)^2,&&n=0,1,2,\ldots\\[3pt] & X_n=\cos \bigl(\frac{\pi n}{l}x\bigr). \end{align}
Example 3 (Dirichlet-Neumann) Eignevalue problem \begin{align} & X'' +\lambda X=0 && 0<x<l,\\[3pt] & X(0)=X'(l)=0 \end{align} has eigenvalues and corresponding eigenfunctions \begin{align} & \lambda_n=\bigl(\frac{\pi (2n+1)}{2l}\bigr)^2,&&n=0,1,2,\ldots\\[3pt] & X_n=\sin \bigl(\frac{\pi (2n+1)}{2l}x\bigr) \end{align} while the same problem albeit with the ends reversed (i.e. $X'(0)=X(l)=0$) has the same eigenvalues and eigenfunctions $\cos \bigl(\frac{\pi (2n+1)}{2l}x\bigr)$.
Example 4 (periodic). Eignevalue problem \begin{align} & X'' +\lambda X=0 && 0<x<l,\\[3pt] & X(0)=X(l), \quad X'(0)=X'(l) \end{align} has eigenvalues and corresponding eigenfunctions \begin{align} & \lambda_0=0,\\[3pt] & X_0=1,\\ & \lambda_{2n}=\lambda_{2n+1}=\bigl(\frac{\pi n}{2l}\bigr)^2,&&n=1,2,\ldots\\[3pt] & X_{2n}=\cos \bigl(\frac{2\pi n}{l}x\bigr), && X_{2n}=\sin \bigl(\frac{2\pi n}{l}x\bigr). \end{align} Alternatively, as all eigenvalues but $0$ have multiplicity $2$ one can select \begin{align} & \lambda_n=\bigl(\frac{2\pi n}{l}\bigr)^2,&&n=\ldots, -2,-1,0, 1,2,\ldots\\[3pt] & X_{n}=\exp \bigl(\frac{2\pi n}{l}i x\bigr). \end{align}
Example 5 (quasiperiodic). Eignevalue problem \begin{align} & X'' +\lambda X=0 && 0<x<l,\\[3pt] & X(0)=e^{-ikl}X(l), \quad X'(0)=X'(l)e^{-ikl}X(l) \end{align} with $0<k<\frac{2\pi}{l}$ has eigenvalues and corresponding eigenfunctions \begin{align} & \lambda_{n}=\bigl(\frac{2\pi n}{l}+k \bigr)^2,&& n=0,2,4,\ldots \\[3pt] & X_{n}=\exp \bigl(\bigl[\frac{2\pi n}{l}+k\bigr]i x\bigr), \\[3pt] & \lambda_{n}=\bigl(\frac{2\pi (n+1)}{l}-k \bigr)^2,&& n=1,3,5,\ldots \\[3pt] & X_{n}=\exp \bigl(\bigl[\frac{2\pi (n+1)}{l}-k\bigr]i x\bigr). \\[3pt] \end{align} This is the simplest example of problems appearing in the description of free electrons in the crystals; much more complicated and realistic example would be Schrödinger equation \begin{equation*} X'' +\bigl(\lambda-V(x)\bigr)X=0 \end{equation*} or its $3D$-analog.
Example 6 (Robin boundary conditions). Consider eignevalue problem \begin{align} & X'' +\lambda X=0 && 0<x<l,\\[3pt] & X'(0)=\alpha X(0), \quad X'(l)=-\beta X(l) \end{align} with $\alpha\ge 0$, $\beta\ge 0$ ($\alpha+\beta>0$). Then \begin{multline} \lambda \int_0^l X^2\,dx=-\int_0^l X''X\,dx =\\ \int_0^l X'^2\,dx-X'(l)X(l) +X'(0)X(0)=\\ \int_0^l X'^2\,dx+\beta X(l)^2 +\alpha X(0)^2\qquad \end{multline} and $\lambda_n=\omega_n^2 $ where $\omega_n>0$ are roots of \begin{align} & \tan (\omega l)= \frac{(\alpha+\beta)\omega}{\omega^2-\alpha\beta};\\ & X_n= \omega \cos (\omega_n x) +\alpha \sin (\omega_n x); \end{align} ($n=1,2,\ldots$)
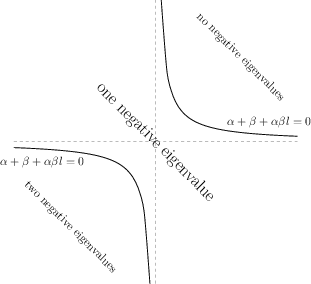
Example 7 (Robin boundary conditions (continued)). However if $\alpha $ and/or $\beta$ are negative, one or two negative eigenvalues $\lambda=-\gamma^2$ can also appear where \begin{align} & \tanh (\gamma l )= {-\frac{(\alpha + \beta)\gamma }{\gamma ^2 + \alpha\beta}},\\ & X(x) = \gamma \cosh (\gamma x) + \alpha \sinh (\gamma x). \end{align}
To investigate when it happens, consider the threshold case of eigenvalue $\lambda=0$: then $X=cx+d$ and plugging into b.c. we have $c=\alpha d$ and $c=-\beta (d+lc)$; this system has non-trivial solution $(c,d)\ne 0$ iff $\alpha+\beta+\alpha\beta l =0$. This hyperbola divides $(\alpha,\beta)$-plane into three zones:
