
$\newcommand{\erf}{\operatorname{erf}}$ $\newcommand{\const}{\mathrm{const}}$
Consider IBVP for 1D-wave equation on $(0,l)$: \begin{align} & u_{tt}-c^2 u_{xx}=0,&& 0<x<l \label{eq-1}\\[3pt] & u|_{x=0}=u|_{x=l}=0, \label{eq-2}\\[5pt] & u|_{t=0}=g(x) && u_t|_{t=0}=h(x). \label{eq-3} \end{align}
Let us skip temporarily initial conditions (\ref{eq-3}) and consider only (\ref{eq-1})--(\ref{eq-2}) and look for a solution in a special form \begin{equation} u(x,t)= X(x) T(t) \label{eq-4} \end{equation} with unknown functions $X(x)$ on $(0,l)$ and $T(t)$ on $(-\infty,\infty)$. We are looking for non-trivial solution $u(x,t)$ which means that $u(x,t)$ is not identically $0$.
Therefore neither $X(x)$ nor $T(t)$ could be identically $0$ either.
Plugging (\ref{eq-4}) into (\ref{eq-1})--(\ref{eq-2}) we get \begin{align*} & X(x) T''(t)=c^2 X''(x)T(t), \\[3pt] & X(0)T(t)=X(l)T(t)=0, \end{align*} which after division by $X(x)T(t)$ and $T(t)$ become \begin{align} & \frac{ T''(t)}{T(t)}=c^2 \frac{X''(x)}{X(x)}, \label{eq-5}\\[3pt] & X(0)=X(l)=0. \label{eq-6} \end{align} Recall, neither $X(x)$ nor $T(t)$ are identically $0$.
In (\ref{eq-5}) the l.h.e. does not depend on $x$ and the r.h.e. does not depend on $t$ and since we have an identity we conclude that
Both expressions do not depend on $x,t$ and therefore they are constant. We rewrite it as two equalities \begin{equation*} \frac{ T''(t)}{T(t)}=-c^2\lambda,\qquad \frac{ X''(x)}{X(x)}=-\lambda \end{equation*} which in turn we rewrite as (\ref{eq-7}) and (\ref{eq-8}): \begin{align} &X'' +\lambda X=0, \label{eq-7}\\[3pt] & X(0)=X(l)=0, \tag{\ref{eq-6}}\\[5pt] & T''+ c^2\lambda T=0. \label{eq-8} \end{align}
Consider BVP (for ODE) (\ref{eq-7})--(\ref{eq-6}). We need to find its solution $X(x)$ which is not identically $0$.
Definition 1. Such solutions are called eigenfunctions and corresponding numbers $\lambda$ eigenvalues (compare with eigenvectors and eigenvalues.)
Proposition. (\ref{eq-7})--(\ref{eq-6}) has eigenvalues and eigenfunctions \begin{align} & \lambda_n = \frac{\pi^2n^2}{l^2}&& n=1,2,\ldots, \label{eq-9}\\[3pt] &X_n(x)=\sin (\frac{\pi n x}{l}). \label{eq-10} \end{align}
Proof. (\ref{eq-9}) is a 2-nd order linear ODE with constant coefficients and to solve it one needs to consider characteristic equation \begin{equation} k^2+\lambda =0 \label{eq-11} \end{equation} and therefore $k_{1,2}=\pm \sqrt{-\lambda}$ and $X= Ae^{\sqrt{-\lambda}x} + Be^{-\sqrt{-\lambda}x}$ (provided $\lambda\ne 0$). Plugging into $X(0)=0$ and $X(l)=0$ we get \begin{align*} &A \qquad +B\qquad = 0,\\ &Ae^{\sqrt{-\lambda}l} + B e^{-\sqrt{-\lambda}l}=0 \end{align*} and this system has a non-trivial solution $(A,B)\ne 0$ if and only if its determinant is $0$: \begin{equation*} \left| \begin{matrix} 1 & 1\\ e^{\sqrt{-\lambda}l} & e^{-\sqrt{-\lambda}l}\end{matrix}\right|=e^{-\sqrt{-\lambda}l}-e^{\sqrt{-\lambda}l}=0 \iff e^{2\sqrt{-\lambda}l} \iff 2\sqrt{-\lambda}l=2\pi in \end{equation*} with $n=1,2,\ldots$. Here we excluded $n=0$ since $\lambda \ne 0$ and both $n$ and $-n$ lead to the same $\lambda$ and $X$. The last equation is equivalent to (\ref{9}). Then $k_{1,2}=\frac{\pi n}{l} i$.
Meanwhlie $B=-A$ anyway and we get $X=2Ai \sin (\frac{\pi n x}{l})$ i.e. (\ref{eq-10}) as factor does not matter.
So far we have not covered $\lambda=0$. But then $k_{1,2}=0$ and $X=A+Bx$ and plugging into (\ref{eq-6}) we get $A=A+Bl=0 \implies A=B=0$ and $\lambda=0$ is not an eigenvalue.
After eigenvalue problem has been solved we plug $\lambda=\lambda_n$ into (\ref{eq-8}): \begin{equation} T''+ (\frac{c\pi n}{l})^2 T=0 \label{eq-12} \end{equation} which is also a 2-nd order linear ODE with constant coefficients.
Characteristic equation $k^2+ (\frac{c\pi n}{l})^2=0$ has solutions $k_{1,2}=\pm \frac{c\pi n}{l}i$ and therefore \begin{equation} T_n(t)=A_n \cos(\frac{c\pi n}{l}t ) + BA_n \sin (\frac{c\pi n}{l}t ) \label{eq-13} \end{equation} and finally \begin{multline} u_n(x,t)= \underbrace{\bigl( A_n \cos(\frac{c\pi n}{l}t )+ B_n \sin (\frac{c\pi n}{l}t )\bigr)}_{=T_n(t)} \cdot \underbrace{\sin (\frac{\pi n x}{l})}_{=X_n(x)}\\ n=1,2,\ldots \label{eq-14} \end{multline}
This simple solution (\ref{eq-14}) represents a standing wave

which one can decompose into a sum of running waves
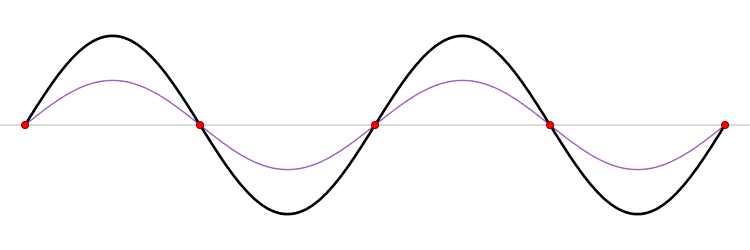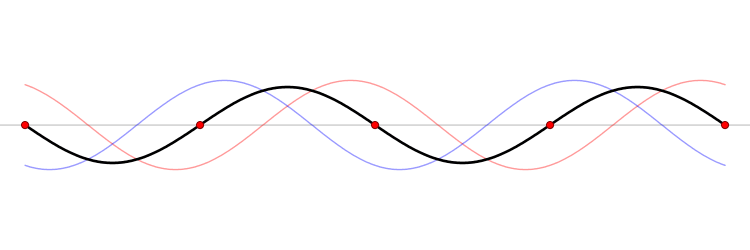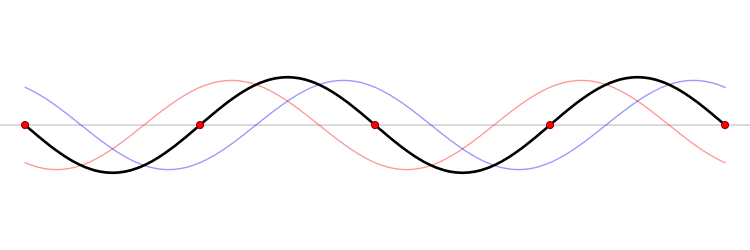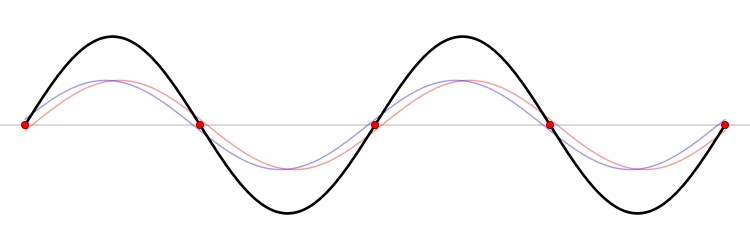
and the general discussion of standing waves could be found in wikipedia
The sum of solutions of \ref{eq-1})-(\ref{eq-2}) is also a solution: \begin{equation} u(x,t)= \sum_{n=1}^\infty \bigl( A_n \cos(\frac{c\pi nt}{l} )+ B_n \sin (\frac{c\pi nt}{l} )\bigr) \cdot \sin (\frac{\pi n x}{l}).\label{eq-15} \end{equation} We have an important question to answer:
Have we covered all solutions of (\ref{eq-1})-(\ref{eq-2})? -- Yes, we did but we need to justify it.
Plugging (\ref{eq-15}) into (\ref{eq-3})1,2 we get respectively \begin{align} &\sum_{n=1}^\infty A_n \sin (\frac{\pi n x}{l})=g(x),\label{eq-16}\\ &\sum_{n=1}^\infty \frac{c\pi n}{l} B_n \sin (\frac{\pi n x}{l} )=h(x). \label{eq-17} \end{align}
How to find $A_n$ and $B_n$? Do they exist? Are they unique?
What we got are Fourier series (actually $\sin$-Fourier series). And we consider their theory in the several next lectures.