2010 04 13 Ionescu Unique Continuation Talk Notes

Some Problems on Unique Continuation Retrieved from "http://wiki.math.toronto.edu/TorontoMathWiki/index.php/2010_04_13_Ionescu_Unique_Continuation_Talk_Notes"

First part will be expository. Then, we will talk about new work connected with general relativity.

[edit] Unique Continuation Background

Suppose    $\Omega_b$ is a set and          $T: C^\infty (\Omega_b) \rightarrow {\mathcal{D}}' (\Omega_b)$. Let's consider  $T(u) = 0$. Suppose      $\Omega_s \subset \Omega_b$. Let's say that      $u_1, u_2$ are solutions and      $u_1 \sim u_2$ in    $\Omega_s$. Can we conclude that

       

1. Lack of Uniqueness. This can be seen for example with the linear wave equation in  $\Omega$ by using finite speed of propagation.
2. Well-Posedness. This is a strong form of uniqueness. If    $u_1$ is 'close' to    $u_2$ in the small set then    $u_1$ and    $u_2$ have to be close in the big set. Perhaps you need to assume a slightly stronger notion of closeness in the small set to obtain a weaker notion of closeness on the big set. This type of result emerges from fixed point approaches to proving uniqueness.
3. Unique Continuation. This is a weak form of uniqueness and should be considered to be a regime in between the first two. Let's look at an example:

 

with            $\Omega_s = B_{1/2} \subset B_2 = \Omega_b \subset {\mathbb{R}}^2$. Then  $u = 0$ in    $\Omega_s$ implies that  $u = 0$ in    $\Omega_b$. Consider then the sequence of functions

     

Observe that    $u_n$ is very small in the small set for large  $n$ but these functions are very big in the big set. Despite having uniqueness, we do not have that closeness on the small set implies closeness on the large set.

Examples of Theorems:

• Theorem (Kato):                $\Omega_b = \{ x \in {\mathbb{R}}^d: |x| > R\}, (\Delta + k^2) u = Vu, V \in L^\infty, k > 0, \lim_{|x| \rightarrow \infty} |x| V(x) = 0.$ If    $u \in L^2$ then  $u = 0$.

This says that the operator  $-\Delta + V$ does not have any negative eigenvalues.

• Another example. Let            $T = (g^{\alpha \beta} \partial_\alpha \partial_\beta + A^\alpha \partial_\alpha + b)$,  $g$ non-degenerate. Let's require        $g \in C^\infty, ~A^\alpha, b \in L^\infty$.

Theorem(Carlemen, Arouszajn):       $u \in H^2_{loc} (\Omega), \Omega \subset {\mathbb{R}}^d$ connected,         $\Delta u = A u + B^\alpha \partial_\alpha u, A, B \in L^\infty_{loc} (\Omega)$ and suppose that

           

Then  $u = 0$ in  $\Omega$. (Strong Uniform Continuation Principle; SUCP).

This has been relaxed to (essentially, AI used quotes around the spaces)            $A \in L^{d/2}, B^\alpha \in L^d, \Delta \sim g^{\alpha \beta}, g^{\alpha \beta} \in Lip$.

• Theorem (Holmgren):      $\Omega_b, \phi: \Omega_b \rightarrow {\mathbb{R}}$ with  $\nabla \phi \neq 0$ and    $\Omega_s = \{ \phi < 0 \}$. Pick a point    $p \in \partial{\Omega_s}.$

If  $Tu = 0, u= 0$ in    $\Omega_s$,      $g^{\alpha \beta}, A^\alpha, B$ real-analytic and        $g^{\alpha \beta} \partial_\alpha \phi(p) \partial_\beta \phi (p) \neq 0$ then  $u = 0$ in a neighborhood of  $p$.

This is an almost perfect theorem except for the hypothesis about real analyticity. This prevents easy application of this theorem in the setting of nonlinear problems.

• Theorem (Hormander): If  $Tu =0$ in    $\Omega_b$,  $u =0$ in    $\Omega_s$,  $\phi$ satisfies the pseudo-convexity condition at p then  $u=0$ in a neighborhood of  $p$.

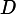
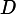
The pseudo-convexity condition is that          $V^\alpha V^\beta D_\alpha D_\beta \phi < 0$ if  $V(\phi) = 0, ~V \neq 0, ~g(V,V) = 0$.

[edit] Towards a Nonlinear Holmgren Theorem

How does one prove a theorem like this? Pseudo-convexity condition is tailored just right to imply Carlemen estimates which then imply Unique Continuation Property. An example of a Carleman estimate in the context of Hörmander's theorem is something like:

                           

Question (nonlinear Holmgren?): Consider      $B_1 \subset {\mathbb{R}}^3$ with coordinates  $(t,x,y)$. Consider the problem

              

 

 

 

Robbiano has proven that the condition    $\partial_t A = 0$ implies uniqueness. Tataru has interpreted this as an interpolation.

Non-uniqueness Theorem: there exist          $u \in C^\infty (B_1), ~A \in C^\infty (B_1)$ and           $(-\partial_t^2 + \partial_x^2 + \partial_y^2) u = Au, ~u =0 =A$ in  $\{ y < 0\}.$ Therefore any progress on this question will somehow have to extract information from the    $u^2$. We would like to prove the Holmgren conclusion holds true for the appropriate class of nonlinear operators.

[edit] New Stuff

(joint work with Alexakis and Klainerman)

Let  $(\Omega,g),$ with  $g$ Lorentzian. We have that    $g \rightarrow D, \rightarrow R_{\alpha \beta \mu \nu} \rightarrow Ric$. The Einstein vacuum equation is that  $Ric = 0$. This emerges from a background problem in which we are interested in final state solutions arising in general relativity. It turns out that many of these solutions have certain symmetries.

Let  $\phi: \Omega \rightarrow {\mathbb{R}}$. Assume  $v$ is smooth and    $\Omega_s = \{ \phi < 0 \}$. Assume we have a Killing vector field in    $\Omega_s$. Can we extend  $V$ to a Killing vector field in  $\Omega$.

Theorem (Alexakis-I-Klainerman): If  $\phi$ satisfies the pseudoconvexity-condition at p then  $V$ extends to a Killing vector field in a neighborhood of that point.

We also have a counterexample that precludes unique continuation through null hypersurfaces.

Theorem ([AIK]): There exists a solution of the vacuum Einstein equations such that the solution is    $g_{kerr}$ on one side of a (null) hypersurface and a different  $g$ on the other side of the hypersurface. We have  $Ric =0$ throughout but the Killing vector fields associated with the Kerr side do not extend across the null hypersurface.