Information
| Instructor | Jean-Baptiste (JB) Campesato |
| campesat [@t) math.toronto.edu | |
| Start the subject with "MAT237:" | |
| Schedule | Tuesday, 6pm to 7pm |
| Thursday, 6pm to 8pm | |
| Room SS2117 | |
| Online via Bb Collaborate | |
| Office Hours | Tuesday, 7pm to 8pm |
| Thursday, 3pm to 4pm | |
| Room PG003 | |
| Online via Bb Collaborate | |
| MAT237 Website | http://uoft.me/MAT237-2019 |
| Official Lecture Notes for MAT237 | http://uoft.me/MAT237-notes |
| My personal notes for each lecture are below | |
| Unfold all lectures | |
| Hide all lectures |
Summary of the Fall TermAll the notes with a table of contents.Slides about level sets (Sep 12). Slides about the Dedekind-completeness of ℝ from Sep 12 Density of ℚ in ℝ Review slides from Oct 10 (section 2.1) Oct 10, reviews questions - Solutions Review slides from Nov 14 (sections 2.2 to 2.7) Nov 14, review questions - Solutions Extra-curricular (difficult, not mandatory): Prove yourself the implicit function theorem and the inverse function theorem using the following questions. Questions - Solutions. Be aware that Questions 2.c. and 4.b. of Exercise 3 are really difficult. Before attempting Question 2.c. you should read "A MVT-like inequality". |
|---|
Summary of the Winter TermAll the notes with a table of contents.Extra-curricular (difficult, not mandatory): Prove the IFTs by yourself - Solutions. Be aware that Questions 2.c. and 4.b. of Exercise 3 are really difficult: you should read "A MVT-like inequality" before attempting Question 2.c. Integration in one variable: reviews from MAT137 My review questions for Test 3 - Sample solutions There may be some mistakes: send me an e-mail if you find something suspicious! Do NOT attempt the difficult questions except if you feel comfortable with the topic. There are too many questions, you don't have to solve all of them. Change of variables: usual coordinate systems (with pictures). A few interesting questions for the reading week - Solutions. Improper integrals in one variable: reviews (updated notes from my MAT137 section last year). Cancellation of the classes: I will continue to update my notes and to maintain this webpage. I will hold my lectures and my office hours online through Bb Collaborate at the usual time slots (a session should appear in the Bb Collaborate section of Quercus a few minutes before). I apologize in advance: we will probably face a few issues concerning the organization or some technical problems (especially the first times). I am also aware that your schedule may have changed a lot with the recent events: do not hesitate to send me e-mails. If necessary, I could also add an extra (online) office hour. Stay safe! My review questions for Test 4 - Solutions. There are a lot of questions, you should probably NOT attempt all of them, that could be too time/energy-consuming. A possible strategy is to attempt questions related to the notions you feel less comfortable with. Another one could be to randomly pick a few questions for each section. I followed the order of the sections in the notes. Be careful: I wrote the solutions in a rush and when we were switching to the online classes (which was time-consuming and stressful). So there are surely mistakes! If you are suspicious about anything, don't waste your time, send me an e-mail. An answer I posted on quercus about the intuition behind line integrals, which I think can be interesting! (the math symbols don't render with Chrome) Le théorème de Stokes dans tous ses états. I added a few historical comments about conservative vector fields in the box for March 19 lecture. The relative boundary in Stokes' theorem. Around Poincaré lemma: a summary of the section about conservative vector fields and vector potentials. A few questions concerning the Gamma function and the Beta function - Solutions. These two functions are defined by improper integrals and they appear in various areas of mathematics. That's not part of MAT237, but, if you have time, I think that could be interesting for your general mathematical knowledge. The last review questions: about sections 5.5, 5.6 and 5.7 - Solutions. Study guide for the final exam: what we did during the review session on April 14. (We went fast so there should be some computation mistakes but the ideas should be OK). |
|---|
Fall Term - Lecture details
| Thursday, September 5 - Show | |
|---|---|
| Files |
Introduction slides In class questions My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Introduction
PreliminariesCartesian product and n-tuples
Functions
Geometry of the Euclidean spaces
|
| Homework |
(That's a lot because it is about reviews, no worries!)
|
| Tuesday, September 10 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
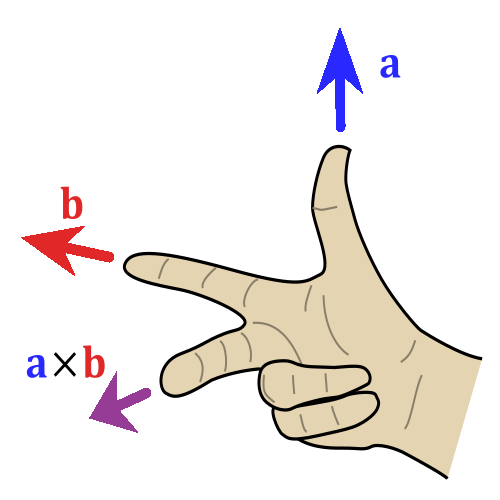
Preliminaries (continuation)Geometry of the Euclidean spaces (continuation)
|
| Homework |
|
| Thursday, September 12 - Show | |
|---|---|
| Files |
Slides: level sets en graphs Slides: in class questions about the interior/closure/boundary of a set - Solutions My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Preliminaries (continuation)How to visualize a several variables function
Some topological notionsBalls and spheres
Interior/Closure/Boundary of a set
|
| Homework |
|
| Tuesday, September 17 - Show | |
|---|---|
| Files |
My notes Solutions to the in class questions (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Some topological notions (continuation)Open and closed sets
Limits of multivariable functions
|
| Homework |
|
| Thursday, September 19 - Show | |
|---|---|
| Files |
My notes - Beware: my "δ" and my "S" look quite similar, but there is no possible confusion: δ is always a positive number and S is always a subset of some Euclidean space. (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Comments and advice |
|
| Content |
Some topological notions (continuation)Limits of multivariable functions
Continuity of multivariable functions
|
| Homework |
|
| Tuesday, September 24 - Show | |
|---|---|
| Files |
Slides about the Dedekind-completeness of the real line Some results about the density of ℚ in ℝ In class questions about the previous lecture (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Homework | Finish the in-class questions. |
| Thursday, September 26 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Some topological notions (continuation)Sequences
Compactness
|
| Homework | Questions from Section 1.4 of the online notes. |
| Tuesday, October 1 - Show | |
|---|---|
| Files |
Some results about the density of ℚ in ℝ My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Some topological notions (continuation)The IVT: path-connected sets
|
| Homework | Questions from Section 1.5 of the online notes. |
| Thursday, October 3 - Show | |
|---|---|
| Files |
My notes (pp. 1-4) Reviews from the future (slides 2 to 6 are interesting for today's lecture) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
DifferentiabilityReal valued functions
|
| Tuesday, October 8 - Show | |
|---|---|
| Files |
My notes (pp. 4-6) Reviews from the future (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Differentiability (continuation)Real valued functions (continuation)
|
| Thursday, October 10 - Show | |
|---|---|
| Files |
My notes (pp. 6-8) Slides (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Differentiability (continuation)Real valued functions (continuation)
|
| Review |
Reviews questions - Solutions Disclaimer: there are too many questions and some are difficult. Do not try to solve all the questions now, but only the ones I explicitely ask you to work on. The questions starting with a star are difficult and I don't suggest you to work on them: they could be useful later for you to deepen the topics when you are confident enough with all the covered material. But I think it could be counterproductive and time-consuming to try to solve them too early. I wrote the solutions very quickly so there may be some mistakes: send me an e-mail if you find one! |
| Homework | Questions from Section 2.1 in the online lecture notes. |
| Tuesday, October 15 - Show | |
|---|---|
| Review |
Reviews questions - Solutions Disclaimer: there are too many questions and some are difficult. Do not try to solve all the questions now, but only the ones I explicitely ask you to work on. The questions starting with a star are difficult and I don't suggest you to work on them: they could be useful later for you to deepen the topics when you are confident enough with all the covered material. But I think it could be counterproductive and time-consuming to try to solve them too early. I wrote the solutions very quickly so there may be some mistakes: send me an e-mail if you find one! |
| Thursday, October 17 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Differentiability (continuation)Linear maps and matrices: recollection
Differentiation of vector-valued functions
|
| Homework | Questions from Section 2.2 of the online notes. |
| Tuesday, October 22 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Differentiability (continuation)The Chain Rule
|
| BEWARE |
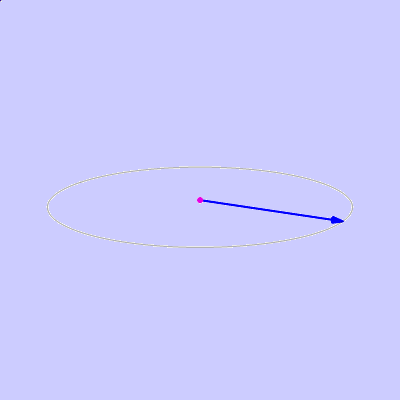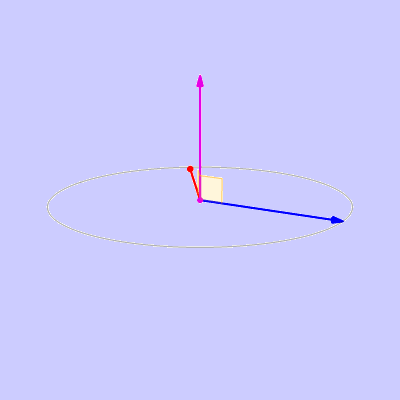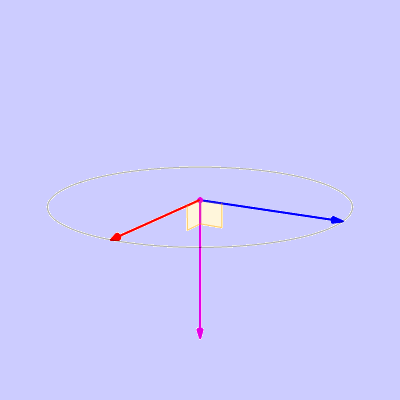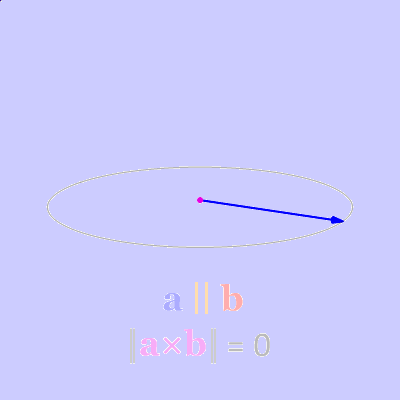
Your worst enemy in calculus is going to be the notation!
|
| Homework | Questions from Section 2.3 of the online notes |
| Thursday, October 24 - Show | |
|---|---|
| Files |
My notes Slides: a summary about differentiability (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Differentiability (continuation)The chain rule (continuation)
The Mean Value Theorem
|
| Homework | Questions from Sections 2.3 and 2.4 in the lecture notes. |
| Tuesday, October 29 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Differentiability (continuation)Higher-order partial derivatives
|
| Homework | Questions from Sections 2.5 of the lecture notes. |
| Thursday, October 31 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Beware: I think that I made TWO mistakes today in class (It looks like that the reading week is necessary for me too...).If I recall correctly, the statement for the multivariable Taylor-Lagrange theorem at order 2 that I wrote on the blackboard is not correct (I added an extra term) and I made a mistake in the proof of the multivariable Taylor-Young (φ can't depend on h).Everything should be fixed in my notes. 🎃👻🍬 and enjoy your reading week. Differentiability (continuation)Taylor's theorem: the one-variable case
Taylor's theorem: the multi-variable case
|
| Homework | Questions from 2.6 (Questions 1 to 4 - "basic skill" only, I don't suggest you to work on the advanced questions for this section). |
|
Reading week: Nov 4 to Nov 8. Reading week reviews: if you want a summary of everything covered in the second part of the lectures! I wrote these slides very very very quickly after the Oct 31 lecture so they probably contain a few typos: please send me an e-mail if something seems wrong! There is no office hours this week (except if you find me here) but I still reply to e-mails. |
|---|
| Tuesday, November 12 - Show | |
|---|---|
| Files |
My notes (pp. 1-3) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Differentiability (continuation)Critical points
|
| Thursday, November 14 - Show | |
|---|---|
| Files |
My notes (pp. 4-7) Review slides Review questions - Solutions (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Differentiability (continuation)Critical points (continuation)
Reviews for Test 2 |
| Homework |
|
| Tuesday, November 19 - Show | |
|---|---|
| Files |
ReviewsReview slidesReview questions - Solutions (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Thursday, November 21 - Show | |
|---|---|
| Files |
My notes (pp. 1-5) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Differentiability (continuity)Optimization with contraints: Lagrange multipliers
|
| Tuesday, November 26 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Differentiability (continuity)Optimization with contraints: Lagrange multipliers
|
| Homework | Question from Section 2.8 of the lecture notes. |
| Thursday, November 28 - Show | |
|---|---|
| Files |
My notes - Lagrange multipliers theorem My notes - the implicit function theorem (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Differentiability (continuation)Lagrange multipliers
The implicit function theorem
|
| Homework | Questions from section 3.1. |
| Tuesday, December 3 - Show | |
|---|---|
| Content |
|
| Homework | Questions from Section 3.1. |
Winter Term - Lecture details
| Tuesday, January 7 - Show | |
|---|---|
| Files |
Introduction slides My notes (pp. 1-3) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
The IFT & the IFTThe Implicit Function Theorem (recollection)
|
| About the proof |
Extra-curricular (difficult, not mandatory): If you are interested in proving the IFT, you can have a look at the following files. Questions - Solutions. Be aware that Questions 2.c. and 4.b. of Exercise 3 are really difficult. Before attempting Question 2.c. you should read "A MVT-like inequality". |
| Homework | Questions from Section 3.1 |
| Thursday, January 9 - Show | |
|---|---|
| Files |
My notes (pp. 4-9) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
The IFT & the IFTThe Inverse Function Theorem
Singular points
|
| About the proof |
Extra-curricular (difficult, not mandatory): If you are interested in proving the IFT, you can have a look at the following files. Questions - Solutions. Be aware that Questions 2.c. and 4.b. of Exercise 3 are really difficult. Before attempting Question 2.c. you should read "A MVT-like inequality". |
| Tuesday, January 14 - Show | |
|---|---|
| Files |
My notes (pp. 10-11) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
The IFT & the IFT (continuation)Singular points (continuation)
|
| Thursday, January 16 - Show | |
|---|---|
| Files |
My notes (pp. 12-21) (I updated my notes since last Tuesday: new material, some typos fixed, and probably some typos added) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
The IFT & the IFT (continuation)Singular points (continuation)
Transformations
|
| Homework | Questions from Section 3.1, 3.2 and 3.3 |
| Tuesday, January 21 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
IntegrationUniform continuity
|
| Homework |
|
| Thursday, January 23 - Show | |
|---|---|
| Files |
My notes (pp. 1-10) Review sheet for the one-variable case: you'll notice that as soon as we define the upper/lower sums for rectangles, there is no difference between the one-variable and multivariable cases. (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
IntegrationSupremum and Infimum (recollection)
Darboux's integral
|
| Homework |
|
| Tuesday, January 28 - Show | |
|---|---|
| Files |
My notes (pp. 10-13 and p16) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Integration (continuation)Darboux's integral (continuation)
|
| Homework | Questions from Section 4.1 and 4.2 |
| Thursday, January 30 - Show | |
|---|---|
| Files |
My review questions for Test 3 - Sample solutions My notes (pp. 16-23) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Integration (continuation)Zero content sets
Integration over a set which is not a rectangle
|
| Homework | Do the exercises about integration of functions not defined on a rectangle |
| Tuesday, February 4 - Show | |
|---|---|
| Files |
My review questions for Test 3 - Sample solutions (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Thursday, February 6 - Show | |
|---|---|
| Files |
My review questions for Test 3 - Sample solutions (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Tuesday, February 11 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Integration (continuation)Iterated integrals
|
| Homework | Questions from Section 4.3 of the online notes |
|
Disclaimer: the next lectures are going to be more computational... The ideas and the methods should be correct. Nevertheless, my computations are true up to a sign, a multiplicative factor and an additive constant. These errors may be cumulative and may appear in various orders. |
|---|
| Thursday, February 13 - Show | |
|---|---|
| Files |
My notes Change of variables: usual coordinate systems (with pictures). (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Integration (continuation)Change of variables
|
| Homework | Questions from Section 4.4 of the online notes |
|
Reading week: Feb 17 to Feb 21. I am not holding office hours this week (except if you find me here on Monday or on Wednesday, or around here on Thursday) but I still reply to e-mails. A few interesting questions for the reading week - Solutions. |
|---|
| Tuesday, February 25 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Integration (continuation)Functions of the form F(x)=∫f(x,y)dy
|
| Homework | |
| Thursday, February 27 - Show | |
|---|---|
| Files |
My notes, pp. 1-9 (updated version with 7 examples that I will explain next Tuesday) Reviews from MAT137: improper integrals in one-variable! (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Integration (continuation)Improper integrals
|
| Homework | Questions from Section 4.5. |
| Tuesday, March 3 - Show | |
|---|---|
| Files |
My notes, pp. 10-∞ (updated version with 7 examples that I will explain next Tuesday) Reviews from MAT137: improper integrals in one-variable! (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Integration (continuation)Improper integrals (continuation)
|
| Homework | Questions from Section 4.5. |
| Thursday, March 5 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Vector calculusLine integrals
|
| Homework | Questions from 5.1. |
| Tuesday, March 10 Show | |
|---|---|
| Files |
My notes (pp. 1-5) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Vector calculus (continuation)Green's theorem
|
| Homework | Questions from 5.2. |
| Thursday, March 12 - Show | |
|---|---|
| Files |
My notes (Green's theorem) My notes (Surface integrals) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Vector calculus (continuation)Green's theorem: examples and applications!
Surface integrals
|
| Homework | Questions from 5.2 and 5.3. |
Cancellation of the classes for the next three weeksAll the new material for my section will be added in the box at the top of the page entitled "Summary of the Winter Term".Particularly, I'll continue to update my notes. The WeBWorK and problem sets will continue as usual. All the necessary information for the continuity of the course will be posted on Quercus as soon as they are available. You can send me questions by e-mail about the content of the course. Work well and stay safe!!! |
|---|
| Tuesday, March 17 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Vector calculus (continuation)Surface integrals (continuation)
|
| Homework | Questions from section 5.3. |
| Thursday, March 19 - Show | |
|---|---|
| Files |
grad/∇, curl/∇×, div/∇· Conservative vector fields and Poincaré lemma (we didn't cover Poincaré lemma in ℝ3 at the end of p5) (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Vector calculus (continuation)grad/∇, curl/∇×, div/∇·
Conservative vector fields and Poincaré lemma
|
| Homework | Questions from section 5.4. |
| Tuesday, March 24 - Show | |
|---|---|
| Files |
Review questions for test 4 - Sample solutions (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Thursday, March 26 - Show | |
|---|---|
| Files |
Review questions for test 4 - Sample solutions (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Tuesday, March 31 - Show | |
|---|---|
| Files |
My notes (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Vector calculus (continuation)The divergence theorem
|
| Homework | Questions from section 5.5 |
| Thursday, April 2 - The Final Lecture - Show | |
|---|---|
| Files |
Slides: the boundary in Stokes' theorem Stokes' theorem Stokes' theorem: all the special cases seen in MAT237 (FTC, Gradient's Theorem, Green's Theorem, Divergence Theorem, Kelvin-Stokes' Theorem) Vector potentials Poincaré lemma: the special cases seen in MAT237 (there are probably some typos and/or mistakes: just send me an e-mail if you think that something is wrong) |
| Content |
Vector calculus (continuation)Stokes' theorem
Vector potentials
|
| Homework | Questions from sections 5.6 and 5.7. |
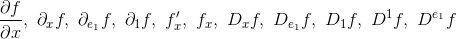
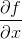 simply denotes the derivative with respect to the first variable (i.e. the directional derivative along e1), do not try to interpret the x in the denominator ∂x.
simply denotes the derivative with respect to the first variable (i.e. the directional derivative along e1), do not try to interpret the x in the denominator ∂x.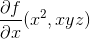 it means that you FIRST compute the partial derivative and THEN that you evaluate it at (x2,xyz). You should NOT compute f(x2,xyz) and then take the derivative with respect to x.
it means that you FIRST compute the partial derivative and THEN that you evaluate it at (x2,xyz). You should NOT compute f(x2,xyz) and then take the derivative with respect to x.